|
| Linear
Equations and Word Problems |
|
|
|
|
Word
problems that lead to simple linear equations |
 Geometry word problems
Geometry word problems |
|
|
|
|
|
|
|
|
Geometry word problems
|
|
The
general procedure to solve a geometry word problem is:
|
| 1.
Draw a sketch of the geometric figure. |
| 2.
Label its elements using information given in the problem. |
| 3.
Choose the correct formula for the
given problem (ex: perimeter, area, volume etc.). |
| 4.
Substitute the data from the problem into the formula. |
| 5.
Solve it for the unknown. |
|
|
|
Example:
The
angle g
of a triangle is twice as large as the
angle a,
and the angle b is
three-fourth of the
|
|
angle g.
What are the angles measures?.
|
| Solution: |
|
given, g
= 2a
and b
= 3/4g
= 3/4 ·
2a =
3/2a |
|
since,
a
+
b +
g
= 180° |
|
then
a
+ 3/2a
+ 2a
= 180° |
|
9/2a
= 180°
=> a
= 40° |
|
b
= 3/2a
= 3/2 ·
40 =
60° |
|
g
= 2a
= 2 · 40°
= 80° |
|
 |
|
|
|
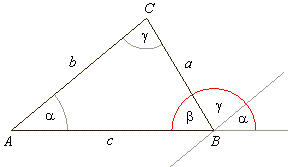
Example: The
exterior angles that lie on the hypotenuse of a right triangle are in the
ratio of 11 : 16, find the angles.
|
| Solution: |
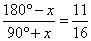 |
|
| 2880 -
16x = 990
+ 11x
|
| 27x = 1890
=> x = a
= 70°,
|
| 180° -
x
= 110°,
90°
+ x =
160°. |
|
 |
|
|
|
Example: In
a circle drawn is a chord whose length is 24 cm and its distance from the
center of the circle is 8 cm less than the radius of the circle. Find the
radius of the circle.
|
| Solution: |
|
r2
=
(r
- 8)2
+ (c/2)2
|
|
r2 = (r - 8)2
+ 122
|
| r2
=
r2
- 16r
+ 64
+ 144
|
| 16r
=
208 |
|
r =
13 cm |
|
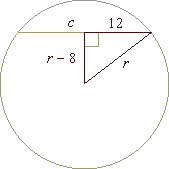 |
|
|
|
|
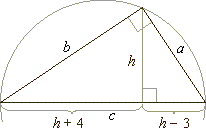
Example: The
height of a right triangle is 3 units longer than the orthogonal projection of
the shorter leg on the hypotenuse and 4 units smaller than the projection of
the longer leg. Find lengths of the projections (segments).
|
| Solution:
Using similarity of the two right triangles, |
|
(h
+ 4)
: h =
h
: (h - 3)
|
| h2 =
(h
+ 4) ·
(h - 3)
|
| h2 = h2
+ h
- 12
=> h
= 12
|
| p
= h - 3
= 12 - 3
= 9, |
| q
= h
+ 4
= 12
+ 4
= 16,
c
= p +
q
= 25 |
|
 |
|
|
|
|
Example: Sides
of a rectangle are in the ratio of 3
: 5. If the length
is decreased by 4 cm and the width is increased by 1 cm, its area will be
decreased by 39 cm2. Find dimensions of the rectangle.
|
| Solution:
a
: b = 3
: 5 => a = (3/5) ·
b |
|
A = a ·
b = (3/5)b
· b
|
| [(3/5)b
+ 1] · (b - 4)
= (3/5)b
· b
- 39
|
|
(3/5)b2
- 7/5b
- 4
= (3/5)b2
- 39 |
|
7/5b =
35,
a = (3/5) ·
b = (3/5) · 35 |
|
b = 25 cm,
a = 15 cm, |
|
 |
|
|
|
|
Example:
If number of sides of a polygon increases by 3 then the number of its
diagonals increases by 18. Which polygon has this properties?
|
|
Solution: Since an
n-sided polygon has
n
vertices, and from each vertex can be drawn (n
- 3)
diagonals, then the total number of diagonals that can be drawn is n
· (n - 3). However,
as each diagonal joins two vertices, this means that each diagonal will be drawn twice, so the expression must be divided by 2.
|
| Thus, number of diagonals of an n-sided
polygon, dn
= n
· (n - 3)
/ 2.
|
|
| By substituting the given condition
|
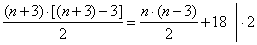
|
| (n
+ 3) · n
= n
· (n - 3)
+ 36
|
|
n2
+ 3n = n2
- 3n
+ 36 |
|
6n = 36
=> n =
6 |
|
 |
|
|
|
|
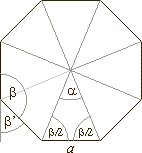
Example:
Of which regular polygon, the difference between the interior and
exterior angle, is 132°.
|
|
Solution:
In a regular polygon a
= 360°/n
and a
+
b
= 180°,
therefore a
= b', as shows the picture.
|
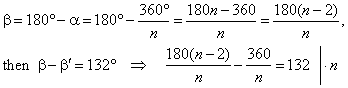
|
|
180n
- 360
- 360 =
132n
|
|
48n
= 720 => n
= 15
|
|
 |
|
|
|
|
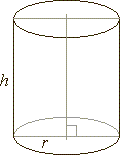
Example:
The ratio of the lateral area of a cylinder to its surface area is 5 :
8. Find the radius of the base if it is 8 cm shorter than the height of the
cylinder.
|
|
Solution: The
lateral area of the cylinder Slat =
2rp
· h = 2rp(r
+ 8),
|
|
and the surface area S =
2B + Slat =
2r2p
+ 2rp(r
+ 8).
|
|
|
given
Slat
: S = 5 :
8
|
|
2rp(r
+ 8)
:
[2r2p
+ 2rp(r
+ 8)] =
5 :
8
|
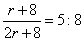
|
|
8r
+ 64 = 10r
+ 40
|
|
2r
= 24 => r
= 12
|
|
 |
|
|
|
|
|
|
|
|
|
|
|
| Intermediate
algebra contents |
|
 |
|
| Copyright
© 2004 - 2020, Nabla Ltd. All rights reserved. |