|
| Linear
Equations and Word Problems |
|
|
|
|
Word
problems that lead to simple linear equations |
Work problems |
|
Time and travel (distance) problems |
|
Miscellaneous word
problems |
|
|
|
|
|
|
| Word
problems that lead to simple linear equations |
| The
general procedure to solve a word problem is: |
| 1.
Set the unknown. |
| 2.
Write equation from the text of the problem. |
| 3.
Solve the equation for the unknown. |
|
|
|
|
Work problems
|
|
Example: One
of two workers can finish a job for 15 days, and other for 10 days, how long
will it take to
|
|
finish the job working together.
|
|
Solution:
The first worker does 1/15 of the job per day, and the second worker does 1/10 of the job per day.
|
|
If working together they complete the job
in x
days, then
|
|
|
|
|
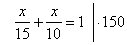
10x + 15x = 150
|
|
25x = 150
|
|
x = 6 days.
|
|
|
Example: Suppose
a person A can finish a job in 12 days. He worked three days when a person B
joins him
|
|
to help. Suppose the person B can finish the same job in 15 days.
How long will they take to finish the job?
|
|
Solution:
If working together they complete the job
in x
days, then
|
|
|
|
|
|
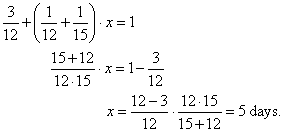
Example: A
tank can be filled with three pipes:
|
|
- first pipe (alone) takes 10 hours (a
= 10) to fill the tank,
|
|
- second pipe takes 12 hours (b
= 12),
|
|
- third pipe takes 15 hours (c
= 15) to fill the tank.
|
|
How long would it take to fill the tank with
water,
|
|
a) if all pipes are opened at the same time,
|
|
b) if second and third pipes fill the tank while at the same time water
leaking from the tank
|
|
through the first pipe?
|
|
Solution: a)
first pipe fills 1/a
part of the tank per hour, second pipe fills 1/b
and third pipe fills 1/c
part of the
|
|
tank per hour. It will take x
hours to fill the thank, thus
|
|
|
|
|
|
|
|
|
|
|
|
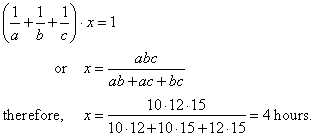
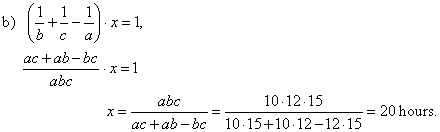
Time and travel problems - Distance, rate (or speed) and time relations
|
|
Use formulas:
|
| distance
= rate ´
time, |
 |
 |
|
|
|
|
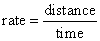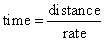Example: A
rider has to catch a pedestrian up who is already 7 hours on his route. How
long it will take if
|
|
the rider travels at the rate of 12 kilometers per hour
and the pedestrian travels at 5 kilometers per hour?
|
|
Solution: The
same distance rider travels x
hours, the pedestrian travels (x
+ 7) hours,
|
|
since, distance
= rate ´
time, then
12 · x =
5 · (x + 7)
|
|
12x = 5x + 35
|
|
7x =
35
|
|
x = 5 hours.
|
|
|
Example: To
travel the distance between two stations a passenger train, traveling at rate
of 12 meters per
second, takes 16 minutes and 40 seconds less than a freight
train moving at speed of 8 meters per second.
|
|
What is the distance?
|
|
Solution: We
equate the times denoting the distance by x,
|
 |
|
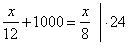where, 16 minutes and 40
seconds = 1000
seconds |
|
|
2x + 2400 = 3x
|
|
x = 24000 meters
= 24 kilometers
|
|
|
Example: A
walker walking at the rate of 1 kilometer in 12 minutes travels a distance from A to
B and spend
|
|
the same time as a cyclist who travels 10 kilometers longer
distance riding at speed of 1 km in four and the
|
|
half minutes. What is the
distance from A to B?
|
|
Solution:
Walker
took a way of x
kilometers at the rate of 1/12 kilometers per minute through the time
|
|
of x/
(1/12) minutes.
|
|
The cyclist travels (x +
10)
kilometers at the rate of 1/(4 and 1/2) kilometers per minute through the time
|
|
of (x +
10) / [1/(4
and 1/2)] minutes.
|
|
They traveled the same period of time, thus
|
|
|
|
|
|
|
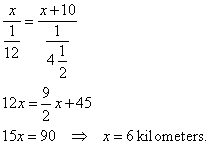
Miscellaneous word
problems
|
|
Example:
If fresh grapes contain 90% water and dried 12%, how much dry grapes we get from 22 kg of fresh
grapes?
|
|
Solution: Fresh grapes contain 90% water and 10% dry substance.
|
|
Dry grapes contain 12% water and 88% dry substance.
|
| 22 kg of fresh grapes = x kg
of dry grapes, so |
 |
|
|
|
|
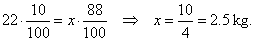Example: An amount decreased 20% and then increased 50%, what is the total increase in relation to initial
value.
|
|
Solution: An initial amount
x decreased by 20%, |
 |
|
|
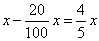The obtained amount increased by 50%, |
 |
|
|
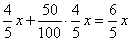The difference in relation to the initial value x,
|
 |
|
|
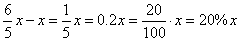shows increase by 20%.
|
|
|
|
Example: From a total deducted is 5% for expenses and the remainder is equally divided to three persons.
|
|
What was the total
if each person gets $190?
|
|
Solution: If
x
denotes the total then |
 |
|
|
|
|
|
|
Example: Into 10 liters of the liquid
A poured is 4 liters of the liquid
B
and 6 liters of the liquid
C.
|
|
From obtained mixture D
poured is out 3 liters, how many liters of the liquid C
remains in the mixture
D?
|
|
Solution: A
+ B
+ C
= D
=> 10 l + 4 l + 6 l = 20 l
|
|
|
|
|
|
|
|
|
|
|
|
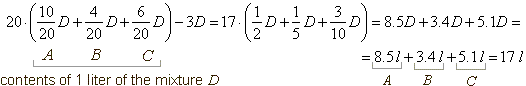
| Intermediate
algebra contents |
|
 |
|
| Copyright
© 2004 - 2020, Nabla Ltd. All rights reserved. |
