|
| Plane Geometry, Plane Figures (Geometric
Figures) - Triangles |
|
|
 Similarity and congruence of
triangles use
Similarity and congruence of
triangles use
|
|
Congruence |
 The
sine law (or the sine rule) and the cosine law
The
sine law (or the sine rule) and the cosine law |
|
The
sine law |
|
The
sine law examples |
|
Solving
the oblique triangle - use of the sine law and the cosine law |
|
|
|
|
|
|
| Congruence
|
| Two triangles are congruent if they have identical size and shape
so that they can be exactly superimposed. |
| Thus, two triangles are
congruent: |
| a) if a pair of corresponding sides and the included
angle are equal, |
| b) if their corresponding sides are
equal, |
| c) if a
pair of corresponding angles and the included side are equal. |
|
| The
sine law
(or the sine rule) and the cosine law |
| From the congruence of triangles follows that an oblique triangle is determined by three of its parts, as are |
| - two sides and the included angle
(SAS), |
| - two angles and the included side
(ASA), |
| - three sides
(SSS) and |
| - two sides and the angle opposite one of them
(SSA), which does not always determine a unique triangle. |
| By using definitions of
trigonometric functions of an acute angle and Pythagoras’ theorem, we can
examine mutual relationships of sides and corresponding angles of an oblique triangle. |
|
| The
sine law |
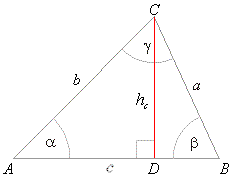
| From
the right triangles,
ACD and
BCD
in the figure, |
| hc
= a sinb
and hc
= b sina, |
| so
that,
a
sinb
= b sina, |
| therefore, |
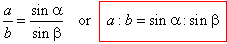 |
|
|
 |
|
| Expressing
the same way the altitudes, hb and
ha as common legs of another
pairs of two right triangles in the given triangle, we get |
| hb
= a sing
and hb
= c sina, |
| so
that,
a sing
= c
sina, |
| or |
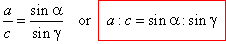 |
|
|
| and,
ha
= b sing
and ha
= c sinb, |
| so
that,
b
sing
= c
sinb, |
| or |
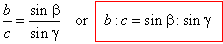 |
|
|
|
| These relations are called the
sine law and in words: |
| Sides of a triangle are to one another in the same
ratio as sine of the corresponding (opposite) angles. |
| As these ratios express relations of any of two sides and their opposite angles, it follows that the sine law
can be applied to solve an oblique triangle in the cases when given are, |
| - two angles and the included side
(ASA) and |
| - two sides and the angle opposite one of them
(SSA), that does not specify a triangle uniquely. |
|
| Example:
In the oblique triangle ABC side
a
= 6 cm, angles,
a
= 38° and g =
120°, find the remaining sides
b
and c
and angle b. |
| Solution: Given
a
= 6 cm, a
= 38° and g
= 120°.
b,
c and
b
= ? |
| As
a
+ b + g =
180°
then b
= 180°
-
(a
+ g) =
180°
-
158°
= 22°,
and since
|
|
|
| Example:
In the oblique triangle with sides,
b = 7 cm and
c
= 4 cm and angle
b
= 115°, find the side
a
and
angles, a
and g. |
| Solution: Given
b = 7 cm, c =
4 cm and b
= 115°.
a,
a and
g
= ? |
| Sequence of calculating the particular part of the triangle depends of the given parts, that
is, use the ratio that
includes all three known parts and the one needed to be
calculated, so
|
|
|
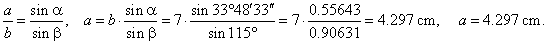 |
|
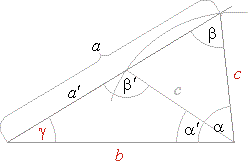
| Example:
In the triangle with sides, b = 7 cm and
c
= 4 cm and angle
g
= 31°11′27″, find the side
a
and angles,
a
and b. |
| Solution: Given
b = 7 cm, c =
4 cm and g
= 31°11′27″.
a,
a
and b
= ? |
| As shows
the below figure it is possible construct two triangles with given parts, one acute, the other obtuse.
|
| That is, the problem has two solutions, one triangle with angle
b
and the other with angle b′
= 180°
-
b.
|
 |
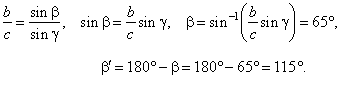 |
|
a
and a′
from, a
+ b + g =
180°
and a′
+ b′ + g =
180°,
|
| so,
a
= 180°
-
(b
+ g) =
180°
-
96°11′27″
= 83°48′33″ |
|
|
|
and a′
= 180°
-
(b′
+ g) =
180°
-
(180° -
b
+ g)
= b
-
g
= 65°
-
31°11′27″
= 33°48′33″.
|
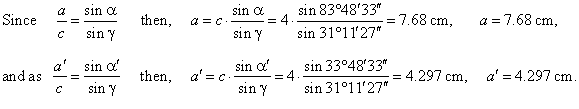 |
|
| Solving
the oblique triangle - use of the sine law and the cosine law |
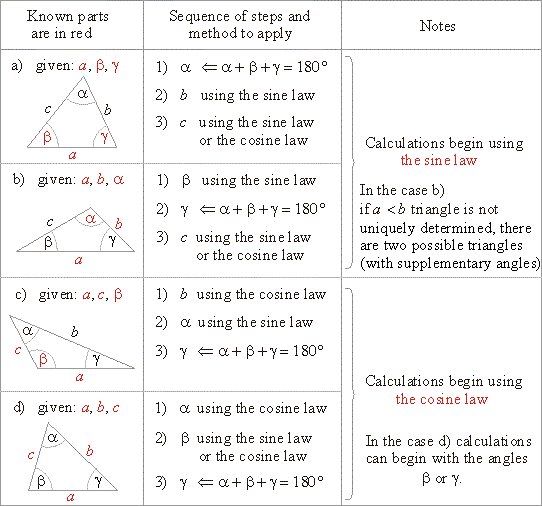 |
|
|
|
|
|
|
|
|
|
|
| Geometry
and use of trigonometry contents - A |
|
 |
|
| Copyright
© 2004 - 2020, Nabla Ltd. All rights reserved. |