|
| Plane Geometry, Plane Figures (Geometric
Figures) - Triangles |
|
|
|
Oblique
or Scalene Triangle |
 Properties and rules
Properties and rules
|
 Perpendicular bisectors,
triangles circumcenter
Perpendicular bisectors,
triangles circumcenter
|
 Angle bisectors, the center of the triangle’s incircle
Angle bisectors, the center of the triangle’s incircle
|
 The
median, the centroid of a triangle
The
median, the centroid of a triangle |
 The altitude of a triangle, orthocenter
The altitude of a triangle, orthocenter
|
 Triangle formulas
Triangle formulas |
 Similarity and congruence of
triangles use
Similarity and congruence of
triangles use
|
|
Congruence |
|
|
|
|
|
|
| Properties and rules
|
| The sum of the angles of a triangle
is a +
b
+ g
= 180°. |
|
Any side of a triangle is shorter than the sum of other two
sides. |
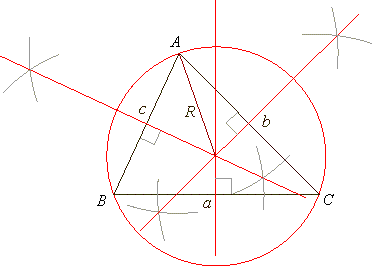
| Circumcircle |
| A
perpendicular bisector of a triangle is a straight line
passing through the midpoint of a side and being perpendicular
to it. |
| The
perpendicular bisectors of the sides of any triangle are concurrent
(all pass through the same point). |
| The perpendicular bisectors intersect in the
triangle's circumcenter. |
| The triangle's circumcenter is the center of the
circumcircle which circumscribes given triangle passing through all its vertices. |
| Acute
triangles' circumcenter falls inside the triangle. Obtuse
triangles' circumcenter falls outside the triangle. |
|
 |
|
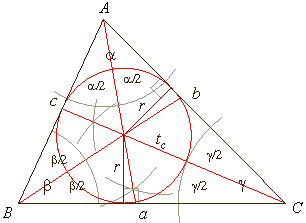
| Incircle |
| An
angle bisector is a straight line through a vertex of a
triangle that divides the angle into two equal parts. |
| The three
angle bisectors intersect in a single point called the incenter,
the center of the triangle's incircle. |
| Incircle
is a circle inscribed in a triangle so that each of the sides of
the triangle is a tangent, of which the radius is inradius,
therefore the radius is perpendicular from the incenter to any
side. |
|
 |
|
| Median
and centroid |
| The
median of a triangle is a straight line through a vertex
and the midpoint of the opposite side, and divides the triangle into
two equal areas. |
| The medians intersect at the triangle's
centroid. |
| The centroid cuts every median in the ratio
2 : 1 from a vertex to the midpoint of the opposite side. |
|
|
|
|
| Altitude
and orthocenter |
| The
altitude of a triangle is a straight line through a vertex and perpendicular to the opposite side. |
| The
altitudes intersect in the orthocenter of the triangle.
See the picture above. |
|
| Triangle
formulas
|
| Meaning
of symbols used in the above pictures and in the triangle
formulas are: h
-altitude, m
-median, t
-angle bisector,
r -radius
of the incircle, R
-radius of the
circumcircle, A
-area, P
-perimeter, s
-semi-perimeter. |
|
|
|
|
|
|
| Similarity and congruence of
triangles use
|
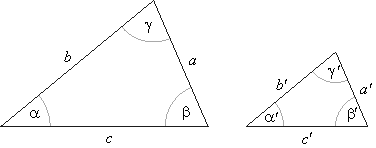
| Similarity
|
| Two triangles (or two plane figures) are similar if they have
corresponding angles equal |
|
a = a', b
= b', g
= g', |
| hence corresponding pairs of sides in
proportion. |
| If
k is the ratio of sides of two similar triangles, then
a'
= ka,
b'
= kb,
c'
= kc, |
| hence |
P'
= kP |
| and |
A'
= k2A |
|
 |
|
|
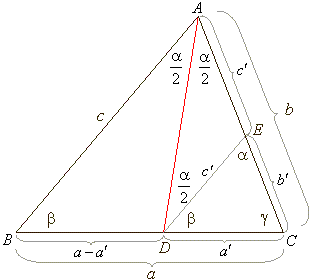
| Example:
Given triangle ABC
is divided by the angle a
bisector into two triangles ABD
and ADC,
as is shown in the picture. |
 |
|
| By
use of the similarity it can be shown that |
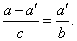 |
| Proof:
Through the point D
drawn is the line segment DE
parallel to the side c,
hence the triangles, ABC
and EDC
are similar. Therefore |
|
|
|
| Example:
Find the value of x
of the triangle shown in the picture. |
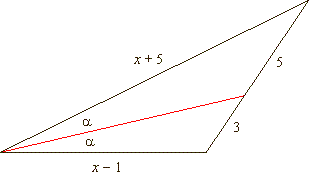 |
| Solution: |
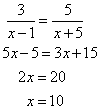 |
|
|
|
|
| Congruence
|
| Two triangles are congruent if they have identical size and shape
so that they can be exactly superimposed. |
| Thus, two triangles are
congruent: |
| a) if a pair of corresponding sides and the included
angle are equal, |
| b) if their corresponding sides are
equal, |
| c) if a
pair of corresponding angles and the included side are equal. |
|
| The
sine law
(or the sine rule) and the cosine law |
| From the congruence of triangles follows that an oblique triangle is determined by three of its parts, as are |
| - two sides and the included angle
(SAS), |
| - two angles and the included side
(ASA), |
| - three sides
(SSS) and |
| - two sides and the angle opposite one of them
(SSA), which does not always determine a unique triangle. |
| By using definitions of
trigonometric functions of an acute angle and Pythagoras’ theorem, we can
examine mutual relationships of sides and corresponding angles of an oblique triangle. |
|
|
|
|
|
|
|
|
|
|
| Geometry
and use of trigonometry contents - A |
|
 |
|
| Copyright
© 2004 - 2020, Nabla Ltd. All rights reserved. |