|
| Plane Geometry, Plane Figures (Geometric
Figures) - Triangles |
|
|
|
|
Similarity and congruence of
triangles use
|
|
Congruence |
|
The
sine law (or the sine rule) and the cosine law |
|
The
cosine law |
|
The
cosine law examples |
|
Calculating angles
of an oblique triangle |
|
Solving
the oblique triangle - use of the sine law and the cosine law |
|
|
|
|
|
|
| Congruence
|
| Two triangles are congruent if they have identical size and shape
so that they can be exactly superimposed. |
| Thus, two triangles are
congruent: |
| a) if a pair of corresponding sides and the included
angle are equal, |
| b) if their corresponding sides are
equal, |
| c) if a
pair of corresponding angles and the included side are equal. |
|
| The
sine law
(or the sine rule) and the cosine law |
| From the congruence of triangles follows that an oblique triangle is determined by three of its parts, as are |
| - two sides and the included angle
(SAS), |
| - two angles and the included side
(ASA), |
| - three sides
(SSS) and |
| - two sides and the angle opposite one of them
(SSA), which does not always determine a unique triangle. |
| By using definitions of
trigonometric functions of an acute angle and Pythagoras’ theorem, we can
examine |
| mutual relationships of sides and corresponding angles of an oblique triangle. |
|
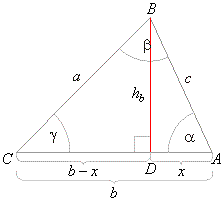
| The cosine law |
| From
the right triangles,
BCD and
ABD
in the figure |
 |
|
 |
|
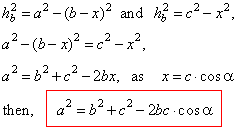| Expressing the same way the squares of the altitudes
as common legs of another two pairs of the right
|
| triangles, obtained are |
 |
|
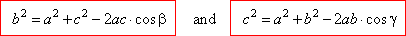| As
in every above formula included are all three sides and the angle that correspond to the
side to be
|
| calculated, of the given oblique triangle, it follows that the
cosine law can be used in the cases if known are, |
| - two sides and the included angle
(SAS) and |
| - three sides
(SSS).
|
|
| Example:
Given is a triangle with sides, a
= 64 cm, c = 29 cm and
angle b
= 147°,
find the side
b, and |
| angles
a and
g. |
| Solution: Given
a
= 64 cm, c
= 29 cm and b
= 147°.
b,
a and
g
= ? Applying
the cosine law |
 |
 |
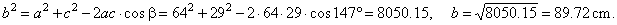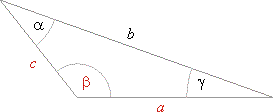| Then,
using the sine law |
 |
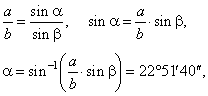| a
+ b + g
= 180°,
g
= 180°
-
(a
+ b)=10°8′20″ |
|
|
|
| Calculating angles
of an oblique triangle |
| The formulas to calculate angles
of an oblique triangle are
derived from the
cosine law, thus |
 |
|
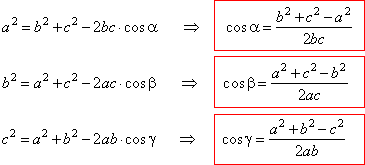| Example:
In a triangle
side, a
= 17 cm, b
= 7 cm and c
= 13 cm, find angles
a ,
b and
g. |
| Solution: Given
a
= 17 cm, b
= 7 cm and c
= 13 cm. a ,
b and
g
= ? Plug the given values into formulas |
|
|
| As
a
+ b + g =
180°
then g
= 180°
-
(a
+ b) =
180°
-
135°14′30″
= 44°45′30″,
g
=
44°45′30″. |
|
| Solving
the oblique triangle - use of the sine law and the cosine law |
 |
|
|
|
|
|
|
|
|
|
|
|
|
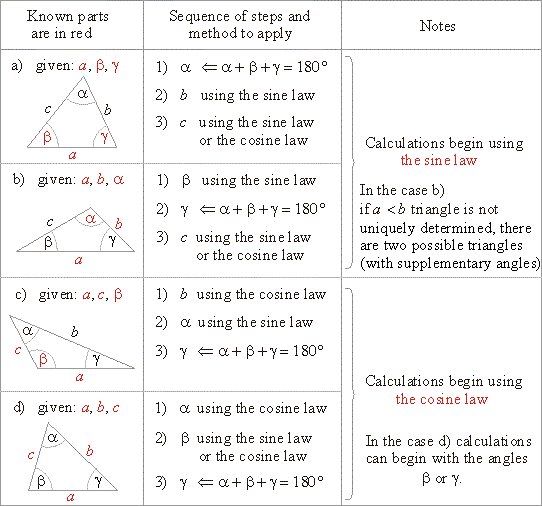| Geometry
and use of trigonometry contents - A |
|
 |
|
| Copyright
© 2004 - 2020, Nabla Ltd. All rights reserved. |
