|
| Applications
of Trigonometry |
|
|
Oblique
or Scalene Triangle |
Mollweide's formulas, the tangent
law (or the tangent rule) and half-angle formulas |
|
The tangent law or the tangent rule |
|
Half-angle formulas |
|
Area of a triangle in terms of the inscribed circle or incircle |
|
The
radius of the inscribed circle |
|
Oblique or scalene triangle
examples |
|
|
|
|
|
|
|
| Oblique
or Scalene Triangle |
| Mollweide's formulas, the tangent
law (or the tangent rule) and half-angle formulas |
 |
|
 |
|
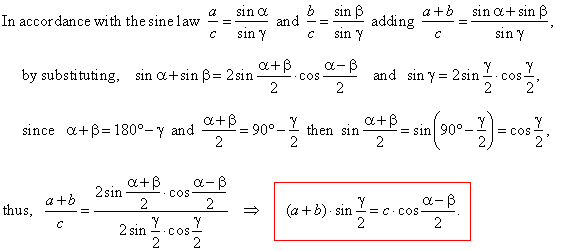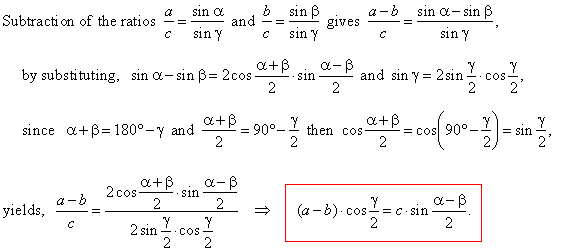| Applying the same procedure on the other propositions of the sine law we derive other
Mollweide's formulas, |
 |
|
|
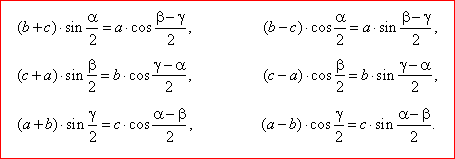The tangent law or the tangent rule |
|
Dividing corresponding pairs of Mollweide's formulas and applying following identities, |
 |
|
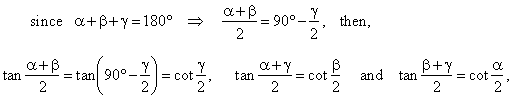obtained are equations that represent the tangent law |
 |
|
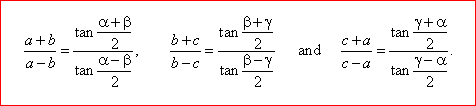| Half-angle formulas |
|
Equating the formula of the cosine law and known identities, that is, |
 |
|
plugged into the above formula gives |
 |
|
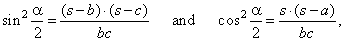dividing above expressions |
 |
|
Applying the same method on the angles, b
and g, obtained are |
 |
|
| Area of a triangle in terms of the inscribed circle (or incircle) radius |
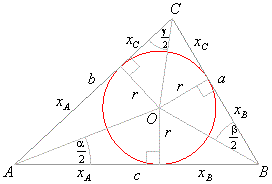
| The oblique triangle
ABC in
the figure below consists of three triangles, ABO,
BCO
and ACO
with the same
altitude r
therefore, its area can be written as |
|
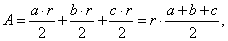
| where |
 |
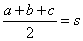is the semi-perimeter |
|
| then |
A
= r
· s |
the
area of a triangle in terms of the |
|
| semi-perimeter and
inradius. |
|
 |
|
|
The parts of a triangle denoted as in the diagram relates as
follows, |
| xA
+ xB
= c,
xA
+ xC
= b,
xB + xC
= a
then, 2xA
= -
(xB + xC) + b + c =
-
a + b + c, |
| 2xB
= a -
(xA + xC) + c =
a -
b + c
and 2xC
= a + b -
(xA
+ xB) + b + c = a + b
-
c, |
| again
using a
+ b + c = 2s
it follows that xA
= s -
a,
xB
= s -
b
and xC
= s -
c. |
|
Then, from the right triangles in the diagram, |
 |
|
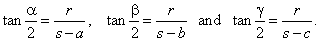Equating obtained formulas with the half-angle formulas, as for example |
 |
|
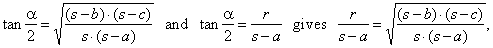or |
 |
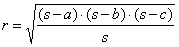the radius of the inscribed circle. |
|
|
Plugging given r
into the formula for the area of a triangle A
= r
· s
yields |
| |
 |
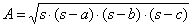Heron's formula. |
|
|
| Oblique or scalene triangle
examples |
| Example:
Determine length of sides, angles and area of a triangle of which
a + b
= 17 cm, c
= 15 cm and
angle g =113°. |
| Solution: Using Mollweide's formula |
 |
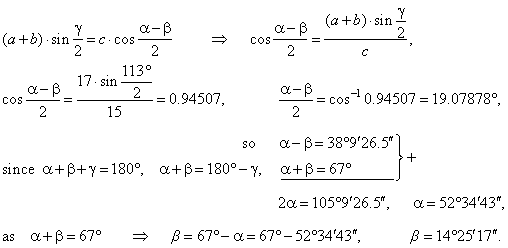| Applying the sine law, |
 |
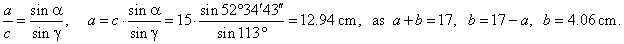| Area of the triangle from the formula |
 |
|
|
|
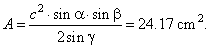| Example:
Given is the sum of the sides of a triangle
a + b +
c = 46 cm, the radius of the incircle
(or inradius) r =
Ö3
cm and angle
b
=60°. Find all sides and angles of the triangle. |
| Solution: Using
the formula |
 |
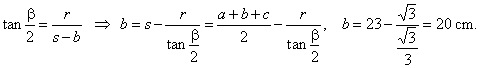| Using Mollweide's formula |
 |
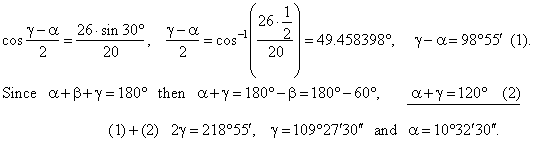| Applying the sine law, |
 |
|
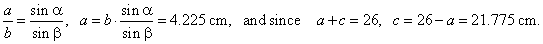| Example:
Determine the area of an isosceles triangle of which, the line segment that joints the midpoint of
one of its equal sides by the midpoint of the base equals the half of the radius
R of the
circumcircle. |
| Solution: In the similar triangles
ABC
and CDE,
b/2 = R/2
=> b = R. |
|
|
| Area of the triangle |
 |
|
|
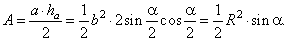Equating obtained formula with the known
formula for the area of a triangle in terms of the radius of the
|
| circumcircle |
 |
|
|
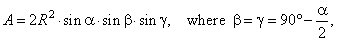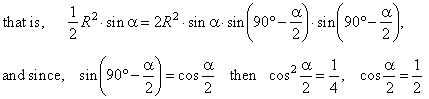
| so, the area of the
triangle |
 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
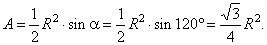| Geometry
and use of trigonometry contents - B |
|
|
 |
|
| Copyright
© 2004 - 2020, Nabla Ltd. All rights reserved. |
