|
| Applications
of Trigonometry |
|
|
|
Oblique
or Scalene Triangle |
Solving oblique triangles - use of
the sine law and the cosine law |
|
Solving oblique triangles examples |
|
|
|
|
|
|
|
|
Oblique
or Scalene Triangle |
| From the congruence of triangles follows that an oblique triangle is determined by three of its parts, as are |
| - two sides and the included angle
(SAS), |
| - two angles and the included side
(ASA), |
| - three sides
(SSS) and |
| - two sides and the angle opposite one of them
(SSA), which does not always determine a unique triangle. |
| By using definitions of
trigonometric functions of an acute angle and Pythagoras’ theorem, we can
examine mutual relationships of sides and corresponding angles of an oblique triangle. |
|
|
| Solving
the oblique triangle - use of the sine law and the cosine law |
 |
|
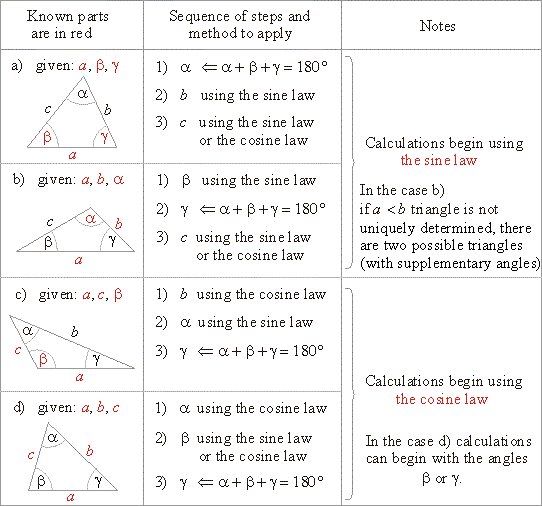| Solving
oblique triangles examples |
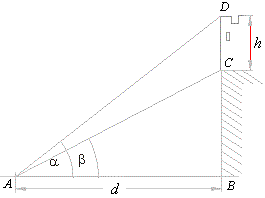
| Example:
From the distance d = 180 m observer sees the top of a castle at the angle of elevation
a =
39° and its bottom at angle
b =
36°. Find the height h of the castle,
see the figure below. |
| Solution:
a) From the right triangle ABC, |
 |
|
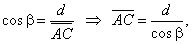| and from the oblique triangle
ACD
using the sine law |
 |
|
 |
|
|
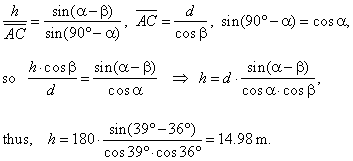b) The same problem can be solved using only a right
triangles.
|
 |
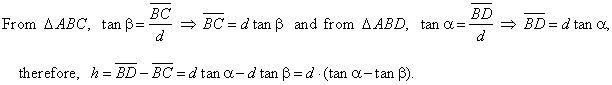| Comparing solutions for
h obtained in a) and b) it follows, |
 |
|
 |
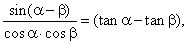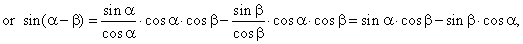| which is known difference formula for sine. |
|
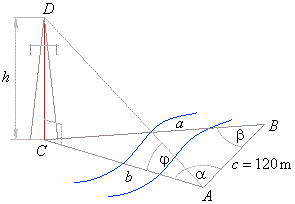
| Example:
From a point A
on a river bank observer sees the top of an electric transmission tower at the
angle of elevation j =
18°. Bottom C, of the tower, and points
A and
B, whose distance is 120 m, forms on the ground triangle with angles
a
= 75° and b
= 62°, as is shown in
the figure below. |
| Find the height
h of the tower. |
| Solution: |
| From the triangle
ABC
by use of the sine law,
|
 |
|
 |
|
|
|
|
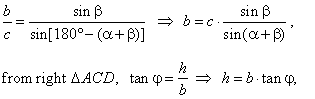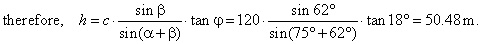
| Example:
Two parallel sides of a trapezoid
a =
12 cm and c
= 5 cm, and side b
= 9 cm, which makes angle
b
= 63° with the side a, see
the figure below. Find the length of the fourth side d, remaining angles, and the area of the
trapezoid. |
| Solution: In triangle
ADE,
d2
= (a
-
c)2
+ b2
-
2(a
-
c)
· b
· cosb |
| d2
= 72
+ 92
-
2
· 7
· 9 · cos63°,
d
= Ö72.8
= 8.53
cm. |
 |
| since
b
+ g
= 180° => g
= 180° -
b
= 117° |
| and
a
+ d
= 180° => d
= 180° -
a
= 109°58′15″. |
|
 |
|
|
|
|
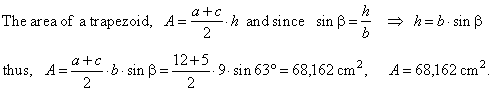
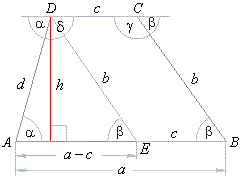
| Example:
An oblique triangle with side
c
= 5 cm and the angles on its ends,
a
= 22° and b
= 125°, rotates
around the given side. Determine the volume and the surface of the solid generated by the rotation. |
| Solution:
The volume of the solid of revolution equals the
difference between the bigger cone of altitude c + h
and
the smaller cone of the altitude h
(a cone dent). |
 |
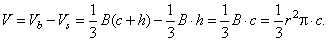Thus, the volume of the solid of revolution equals the
volume of the cone with base in the vertex
B of the triangle
and the height
c. |
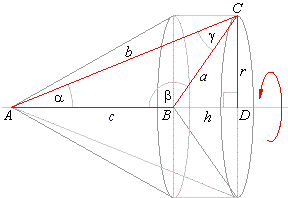
| While, the surface of the solid of revolution
equals the sum of the lateral surfaces of both cones.
|
| S
= Slat.b. + Slat.a.
= rpb
+ rpa
= rp(b
+ a) |
|
 |
|
|
Therefore, we need to calculate the slant height
a
and b
(i.e., sides of the triangle) and radius
r.
|
|
Since a
+ b
+ g
= 180° => g
= 180° -
(a
+ b),
and by using the sine law
|
|
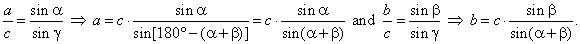
| In the right
DACD, |
 |
|
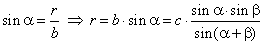| by plugging
the value for r into the formula for the volume
and the formula for for the surface, |
 |
|
|
|
|
|
|
|
|
|
|
|
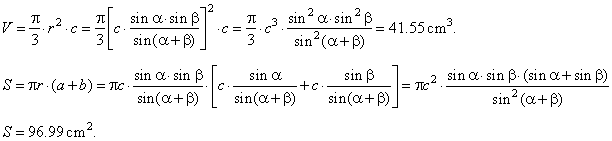| Geometry
and use of trigonometry contents - B |
|
|
 |
|
| Copyright
© 2004 - 2020, Nabla Ltd. All rights reserved. |
