|
| Applications
of Trigonometry |
|
|
Oblique
or Scalene Triangle |
 The cosine
law (rule)
or
the law of
cosines
The cosine
law (rule)
or
the law of
cosines |
|
Calculating angles
of an oblique triangle |
|
Solving oblique triangles examples |
|
|
|
|
|
|
|
Oblique
or Scalene Triangle |
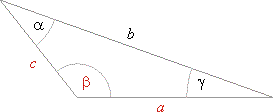
| From the congruence of triangles follows that an oblique triangle is determined by three of its parts, as are |
| - two sides and the included angle
(SAS), |
| - two angles and the included side
(ASA), |
| - three sides
(SSS) and |
| - two sides and the angle opposite one of them
(SSA), which does not always determine a unique triangle. |
| By using definitions of
trigonometric functions of an acute angle and Pythagoras’ theorem, we can
examine mutual relationships of sides and corresponding angles of an oblique triangle. |
|
|
| The cosine law |
| From
the right triangles,
BCD and
ABD
in the figure |
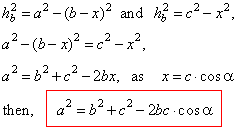 |
|
 |
|
| Expressing the same way the squares of the altitudes
as common legs of another two pairs of the right triangles, obtained are |
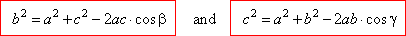 |
|
| As
in every above formula included are all three sides and the angle that correspond to the
side to be calculated, of the given oblique triangle, it follows that the
cosine law can be used in the cases if known are, |
| - two sides and the included angle
(SAS) and |
| - three sides
(SSS).
|
|
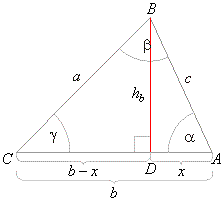
| Example:
Given is a triangle with sides, a
= 64 cm, c = 29 cm and
angle b = 147°, find the side
b, and angles
a and
g. |
| Solution: Given
a
= 64 cm, c
= 29 cm and b
= 147°.
b,
a and
g
= ? Applying
the cosine law |
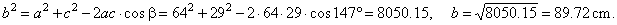 |
 |
| Then,
using the sine law |
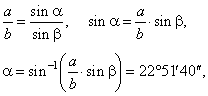 |
| As
a
+ b + g
= 180°,
g
= 180°
-
(a
+ b) =
10°8′20″ |
|
|
|
| Calculating angles
of an oblique triangle |
| The formulas to calculate angles
of an oblique triangle are
derived from the
cosine law, thus |
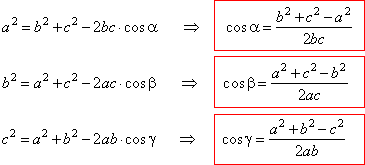 |
|
| Example:
In a triangle
side, a
= 17 cm, b
= 7 cm and c
= 13 cm, find angles
a ,
b and
g. |
| Solution: Given
a
= 17 cm, b
= 7 cm and c
= 13 cm. a ,
b and
g
= ? Plug the given values into formulas |
|
|
| As
a
+ b + g =
180°
then g
= 180°
-
(a
+ b) =
180°
-
135°14′30″
= 44°45′30″,
g
= 44°45′30″. |
|
| Solving
oblique triangles examples |
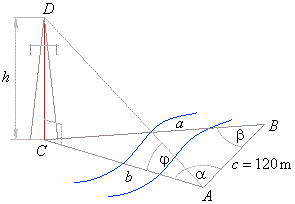
| Example:
From a point A
on a river bank observer sees the top of an electric transmission tower at the
angle of elevation j =
18°. Bottom C, of the tower, and points
A and
B, whose distance is 120 m, forms on the ground triangle with angles
a
= 75° and b
= 62°, as is shown in
the figure below. |
| Find the height
h of the tower. |
| Solution: |
| From the triangle
ABC
by use of the sine law,
|
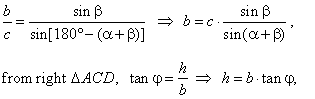 |
|
 |
|
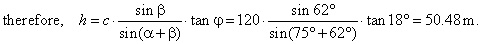
|
|
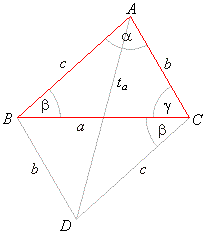
| Example:
Given are sides, a,
b
and c
of a triangle. Find the length of the median ta. |
| Solution: Median
ta
is a half of the diagonal AD
of the parallelogram ABCD, |
| since
a
+ b
+ g
= 180° => b
+ g
= 180° -
a,
according to |
| the cosine law,
(2ta)2
= b2
+ c2
-
2bc
· cos(180°
-
a) |
| then
4ta2
= b2
+ c2
+
2bc
· cos
a, |
| from given triangle
a2
= b2
+ c2
-
2bc
· cos
a, |
| and by adding these two equations,
4ta2
+ a2
= 2(b2
+ c2) |
| obtained is, |
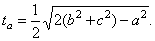 |
|
|
 |
|
|
|
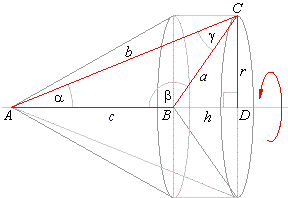
| Example:
An oblique triangle with side
c
= 5 cm and the angles on its ends,
a
= 22° and b
= 125°, rotates
around the given side. Determine the volume and the surface of the solid generated by the rotation. |
| Solution: The volume of the solid of revolution equals the
difference between the bigger cone of altitude c + h
and
the smaller cone of the altitude h
(a cone dent). |
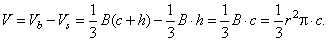 |
Thus, the volume of the solid of revolution equals the
volume of the cone with base in the vertex
B of the triangle
and the height
c. |
| While, the surface of the solid of revolution
equals the sum of the lateral surfaces of both cones.
|
| S
= Slat.b. + Slat.a.
= rpb
+ rpa
= rp(b
+ a) |
|
 |
|
|
Therefore, we need to calculate the slant height
a
and b
(i.e., sides of the triangle) and radius
r.
|
|
Since a
+ b
+ g
= 180° => g
= 180° -
(a
+ b),
and by using the sine law
|
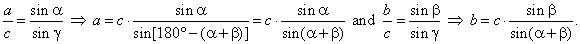
|
| In the right
DACD, |
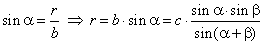 |
|
| by plugging
the value for r into the formula for the volume
and the formula for the surface, |
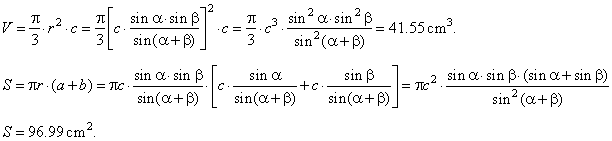 |
|
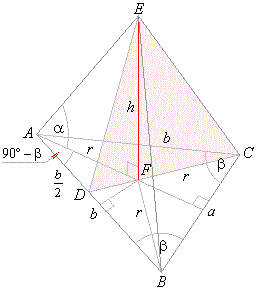
| Example:
Base of a pyramid is an isosceles triangle whose equal sides are
b
and their corresponding (opposite) angles b
(b >
45°). All lateral edges of the pyramid are
equal and make angle a
with the base. |
| The
pyramid is cut by the plane which
passes through the altitude of the pyramid and the vertex of the angle b of the base, see
the below figure.
Determine the area of the section. |
| Solution: The area of the section equals the area of triangle
CDE, that is,
A =
(1/2) · CD
· h |
|
Since the lateral edges are equal, the height h
of the pyramid intersects the base at its circumcentre. |
| Thus,
in right triangle AEF, the height
h
and radius r
of the circumcircle are its legs, that is |
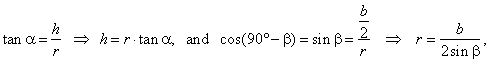 |
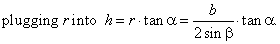 |
| From the oblique triangle whose angles are
|
| CAD
= 180°
-
2b
and DCA
= 90°
-
b, |
| ADC
= 180°
-
[(180°
-
2b)
+ (90°
-
b)]
= 3b
-
90°, |
| using
the
sine law
|
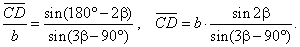 |
| Let
plug the calculated values into the
formula for the section |
|
 |
|
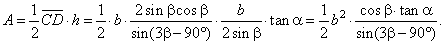 |
|
| Example:
The crane in the below
figure is loaded by the force FL =
25000 N. Crane arms are inclined at
angles a
= 38° and
b
= 57° to the horizontal. Find forces
Fk1
and Fk2 in arms of the crane and force components,
FH
and FN in the point
A. |
| Solution: Angles
in the triangle BCD, angle
BDC
= 90°
-
b,
angle
DCB
= b
-
a
and angle CBD
= 90°
+ a,
thus, using the sine law |
|
|
|
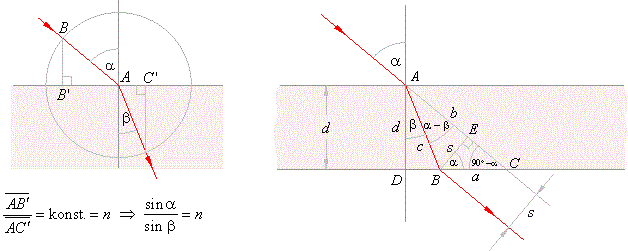
| Example:
A ray of light in air is approaching the glass layer surface at the angle of an incidence
a
= 62°. |
| Find the parallel shift
s
of the ray when exiting the layer thick d =
15 mm, if the index of refraction for glass
n =
1.75. |
| Solution: It is experimentally proved that the ratio between the projection of the part of an incident
ray and the part of a refracted ray, approaching the boundary of two different media, called the index of
refraction is
constant. n,
|
 |
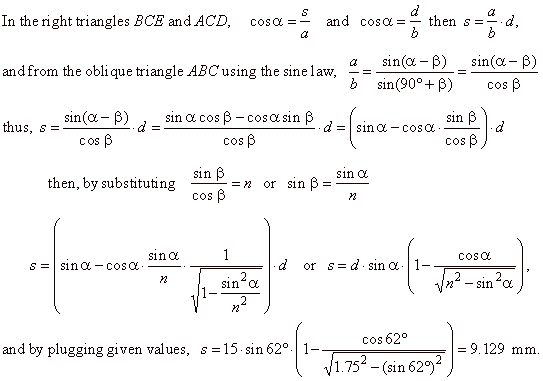 |
|
|
|
|
|
|
|
|
|
|
|
|
| Geometry
and use of trigonometry contents - B |
|
|
 |
|
| Copyright
© 2004 - 2020, Nabla Ltd. All rights reserved. |