|
| Applications
of Trigonometry |
|
|
|
Oblique
or Scalene Triangle |
 The sine law
(rule) or the law of sines
The sine law
(rule) or the law of sines |
 Solving
oblique triangles - use of the sine law and the cosine law
Solving
oblique triangles - use of the sine law and the cosine law |
|
Solving oblique triangles examples |
|
|
|
|
|
|
|
Oblique
or Scalene Triangle |
| From the congruence of triangles follows that an oblique triangle is determined by three of its parts, as are |
| - two sides and the included angle
(SAS), |
| - two angles and the included side
(ASA), |
| - three sides
(SSS) and |
| - two sides and the angle opposite one of them
(SSA), which does not always determine a unique triangle. |
| By using definitions of
trigonometric functions of an acute angle and Pythagoras’ theorem, we can
examine mutual relationships of sides and corresponding angles of an oblique triangle. |
|
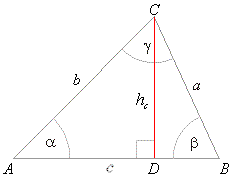
| The
sine law |
| From
the right triangles,
ACD and
BCD
in the figure, |
| hc
= a sinb
and hc
= b sina, |
| so
that,
a
sinb
= b sina, |
| therefore, |
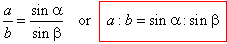 |
|
|
 |
|
| Expressing
the same way the altitudes, hb and
ha as common legs of another
pairs of two right triangles in the given triangle, we get |
| hb
= a sing
and hb
= c sina, |
| so
that,
a sing
= c sina, |
| or |
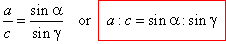 |
|
|
| and,
ha
= b sing
and ha
= c sinb, |
| so
that,
b
sing
= c sinb, |
| or |
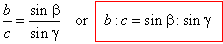 |
|
|
|
| These relations are called the
sine law and in words: |
| Sides of a triangle are to one another in the same
ratio as sine of the corresponding (opposite) angles. |
| As these ratios express relations of any of two sides and their opposite angles, it follows that the sine law can be applied to solve an oblique triangle in the cases when given are, |
| - two angles and the included side
(ASA) and |
| - two sides and the angle opposite one of them
(SSA), that does not specify a triangle uniquely. |
|
| Example:
In the oblique triangle ABC side
a
= 6 cm, angles,
a
= 38° and g =
120°, find the remaining sides
b
and c
and angle b. |
| Solution: Given
a
= 6 cm, a
= 38° and g
= 120°. b,
c and
b
= ? |
| As
a
+ b + g =
180°
then b
= 180°
-
(a
+ g) =
180°
-
158°
= 22°,
and since
|
|
|
|
| Example:
In the oblique triangle with sides, b = 7 cm and
c
= 4 cm and angle
b
= 115°, find the side
a
and
angles, a
and g. |
| Solution: Given
b = 7 cm, c =
4 cm and b
= 115°.
a,
a and
g
= ? |
| Sequence of calculating the particular part of the triangle depends of the given parts, that
is, use the ratio that
includes all three known parts and the one needed to be
calculated, so
|
|
|
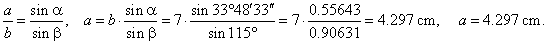 |
|
| Example:
In the triangle with sides, b = 7 cm and
c
= 4 cm and angle
g
= 31°11′27″, find the side
a
and angles,
a
and b. |
| Solution: Given
b = 7 cm, c =
4 cm and g
= 31°11′27″.
a,
a
and b
= ? |
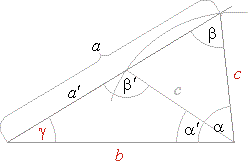
| As shows
the below figure it is possible construct two triangles with given parts, one acute, the other obtuse.
|
| That is, the problem has two solutions, one triangle with angle
b
and the other with angle b′
= 180°
-
b.
|
 |
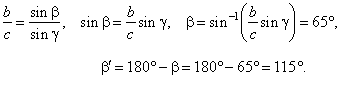 |
|
a
and a′
from, a
+ b + g =
180°
and a′
+ b′ + g =
180°,
|
| so,
a
= 180°
-
(b
+ g) =
180°
-
96°11′27″
= 83°48′33″ |
|
|
|
and a′
= 180°
-
(b′
+ g) =
180°
-
(180° -
b
+ g)
= b
-
g
= 65°
-
31°11′27″
= 33°48′33″.
|
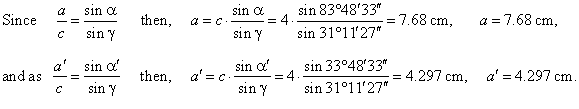 |
|
|
| Solving
the oblique triangle - use of the sine law and the cosine law |
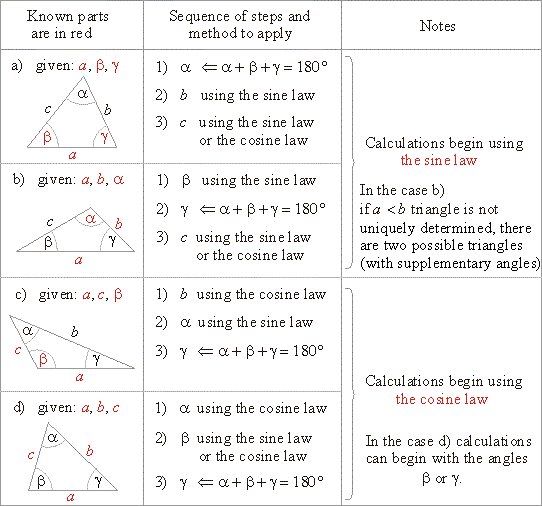 |
|
| Example:
From the distance d = 180 m observer sees the top of a castle at the angle of elevation
a =
39° and its bottom at angle
b =
36°. Find the height h of the castle,
see the figure below. |
| Solution:
a) From the right triangle ABC, |
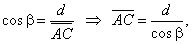 |
|
| and from the oblique triangle
ACD
using the sine law |
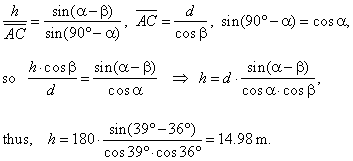 |
|
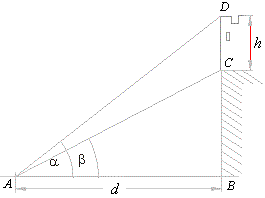 |
|
|
b) The same problem can be solved using only a right
triangles.
|
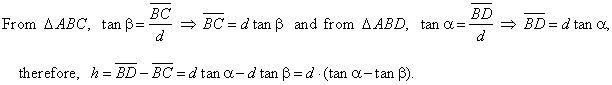 |
| Comparing solutions for
h obtained in a) and b) it follows, |
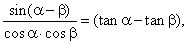 |
|
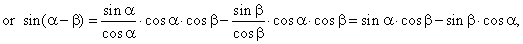 |
| which is known difference formula for sine. |
|
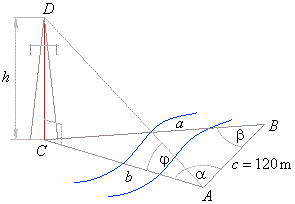
| Example:
From a point A
on a river bank observer sees the top of an electric transmission tower at the angle of elevation
j =
18°. Bottom C, of the tower, and points
A and
B, whose distance is 120 m, forms on the ground triangle with angles
a
= 75° and b
= 62°, as is shown in
the figure below. Find the height
h of the tower. |
| Solution: |
| From the triangle
ABC
by use of the sine law,
|
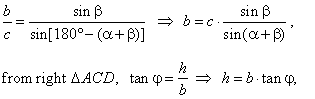 |
|
 |
|
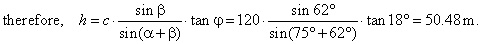
|
|
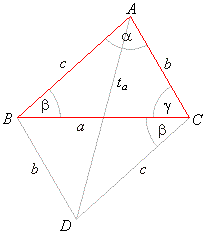
| Example:
Given are sides, a,
b
and c
of a triangle. Find the length of the median ta. |
| Solution: Median
ta
is a half of the diagonal AD
of the parallelogram ABCD, |
| since
a
+ b
+ g
= 180° => b
+ g
= 180° -
a,
according to |
| the cosine law,
(2ta)2
= b2
+ c2
-
2bc
· cos(180°
-
a) |
| then
4ta2
= b2
+ c2
+
2bc
· cos
a, |
| from given triangle
a2
= b2
+ c2
-
2bc
· cos
a, |
| and by adding these two equations,
4ta2
+ a2
= 2(b2
+ c2) |
| obtained is, |
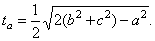 |
|
|
 |
|
|
|
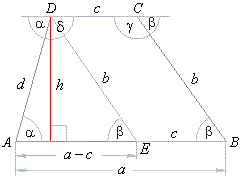
| Example:
Two parallel sides of a trapezoid
a =
12 cm and c
= 5 cm, and side b
= 9 cm, which makes angle
b
= 63° with the side a, see
the figure below. Find the length of the fourth side d, remaining angles, and the area of the
trapezoid. |
| Solution: In triangle
ADE,
d2
= (a
-
c)2
+ b2
-
2(a
-
c)
· b
· cosb |
| d2
= 72
+ 92
-
2
· 7
· 9 · cos63°,
d
= Ö72.8
= 8.53
cm. |
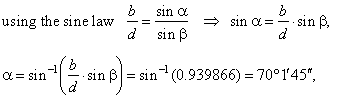 |
| since
b
+ g
= 180° => g
= 180° -
b
= 117° |
| and
a
+ d
= 180° => d
= 180° -
a
= 109°58′15″. |
|
 |
|
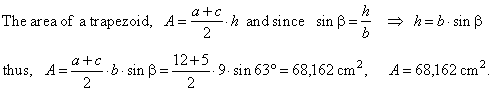
|
|
|
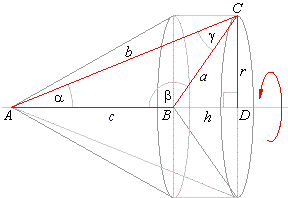
| Example:
An oblique triangle with side
c
= 5 cm and the angles on its ends,
a
= 22° and b
= 125°, rotates
around the given side. Determine the volume and the surface of the solid generated by the rotation. |
| Solution: The volume of the solid of revolution equals the
difference between the bigger cone of altitude c + h and
the smaller cone of the altitude h
(a cone dent). |
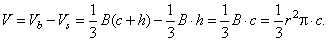 |
Thus, the volume of the solid of revolution equals the
volume of the cone with base in the vertex
B of the triangle
and the height
c. |
| While, the surface of the solid of revolution
equals the sum of the lateral surfaces of both cones.
|
| S
= Slat.b. + Slat.a.
= rpb
+ rpa
= rp(b
+ a) |
|
 |
|
|
Therefore, we need to calculate the slant height
a
and b
(i.e., sides of the triangle) and radius
r.
|
|
Since a
+ b
+ g
= 180° => g
= 180° -
(a
+ b),
and by using the sine law
|
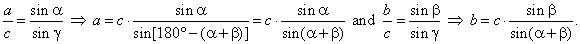
|
| In the right
DACD, |
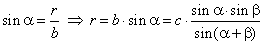 |
|
| by plugging
the value for r into the formula for the volume
and the formula for for the surface, |
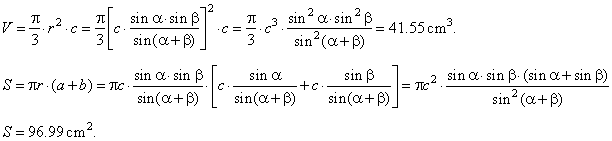 |
|
|
|
|
|
|
|
|
|
|
|
| Geometry
and use of trigonometry contents - B |
|
|
 |
|
| Copyright
© 2004 - 2020, Nabla Ltd. All rights reserved. |