|
| Applications
of Trigonometry |
|
|
|
Right-angled
Triangle or Right Triangle |
 Trigonometric functions of an acute angle defined in a right triangle
Trigonometric functions of an acute angle defined in a right triangle
|
 Solving right triangles
Solving right triangles |
|
Solving right triangles
examples |
|
|
|
|
|
|
|
Right-angled
Triangle
or Right Triangle |
| Trigonometric functions of an acute angle defined in a right triangle
|
| Trigonometric
functions of an acute angle are defined in a right triangle as a
ratio of its sides. |
|
|
|
|
|
| Solving
the right triangle |
| To
solve a right triangle means to find all unknown sides and
angles using its known parts. |
| While
solving a right triangle we use Pythagoras’
theorem and trigonometric functions
of an acute angle depending
which pair of its parts is given |
| Note,
right triangles are usually denoted as follows; c
stands for the hypotenuse, a
and b
for the perpendicular
sides called legs, and a
and b
for the angles opposite to a
and b
respectively. |
| There
are four basic cases that can occur, given |
| a)
hypotenuse and angle, c)
hypotenuse and leg, |
|
b)
leg and angle,
d) two legs. |
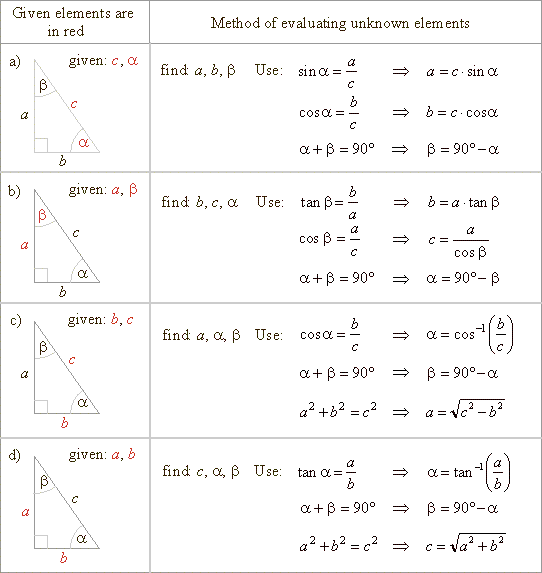 |
|
| Solving right triangles examples |
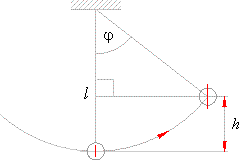
| Example:
Which highest level h will reach a bob pendulum of length
l, starting from rest, where
j is the largest angle attained by the pendulum. |
| Solution: Given
l and
j.
h
= ? |
| From the right triangle in
the right figure |
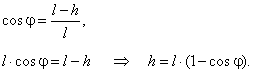 |
|
 |
|
|
|
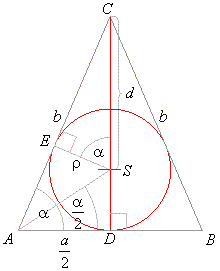
| Example:
In an isosceles triangle two equal sides subtend angles
a
at the endpoints of the third side. |
| What is the length of the third side if the difference between the altitude of the triangle to that side, and the radius of the inscribed circle, equals
d? |
| Solution: Given
a and
d.
a = ? |
| angle
ESC
= angle
EAD
= a
- the angles with mutually perpendicular sides |
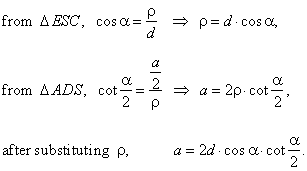 |
|
 |
|
|
| Example:
From a distance an observer sees the top of a church tower at the angle of elevation a = 18°9′34″
when comes 100 m closer, under the angle
b
= 28°39′50″. Find the height
h
of the church and
the distance x. |
| Solution: From the
two right triangles |
|
|
|
|
| Example:
Find the angle a
between a lateral edge and the base, and the base-to-face dihedral angle
b of the regular tetrahedron shown in
the figure below. |
| Solution: R -the radius of circumscribed circle,
r
-the radius of inscribed circle, h
-height of the tetrahedron and ha -height of a face
(the equilateral triangle). |
|
|
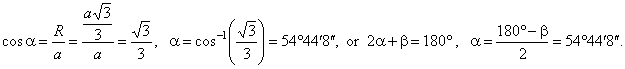
|
|
|
|
|
|
|
|
|
|
|
|
| Geometry
and use of trigonometry contents - B |
|
|
 |
|
| Copyright
© 2004 - 2020, Nabla Ltd. All rights reserved. |