|
| Applications
of Trigonometry |
|
|
|
Right-angled
Triangle or Right Triangle |
Trigonometric functions of an acute angle defined in a right triangle
|
Solving right triangles |
|
Solving right triangles
examples |
|
|
|
|
|
|
|
Right-angled
Triangle
or Right Triangle |
| Trigonometric functions of an acute angle defined in a right triangle
|
| Trigonometric
functions of an acute angle are defined in a right triangle as a
ratio of its sides. |
|
|
|
|
|
| Solving
the right triangle |
| To
solve a right triangle means to find all unknown sides and
angles using its known parts. |
| While
solving a right triangle we use Pythagoras’
theorem and trigonometric functions
of an acute angle depending
which pair of its parts is given. |
| Note,
right triangles are usually denoted as follows; c
stands for the hypotenuse, a
and b
for the perpendicular
sides called legs, and a
and b
for the angles opposite to a
and b
respectively. |
| There
are four basic cases that can occur, given |
| a)
hypotenuse and angle, c)
hypotenuse and leg, |
|
b)
leg and angle,
d) two legs. |
 |
|
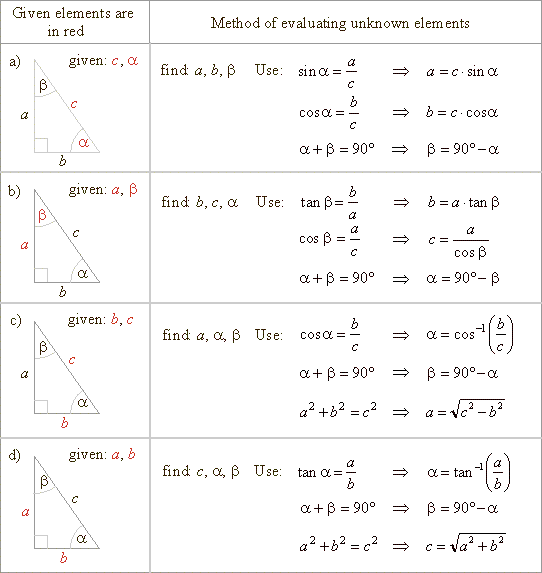| Solving right triangles examples |
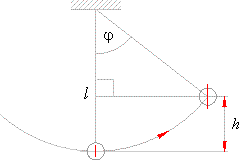
| Example:
Which highest level h will reach a bob pendulum of length
l, starting from rest, where
j is the largest angle attained by the pendulum. |
| Solution: Given
l and
j.
h
= ? |
| From the right triangle in
the right figure |
 |
|
 |
|
|
|
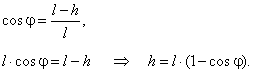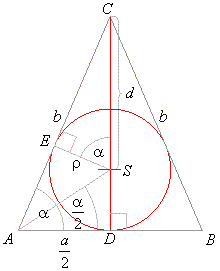
| Example:
In an isosceles triangle two equal sides subtend angles
a
at the endpoints of the third side. |
| What is the length of the third side if the difference between the altitude of the triangle to that side, and the radius of the inscribed circle, equals
d? |
| Solution: Given
a and
d.
a = ? |
| angle
ESC
= angle
EAD
= a
- the angles with mutually |
| perpendicular sides |
 |
|
 |
|
|
|
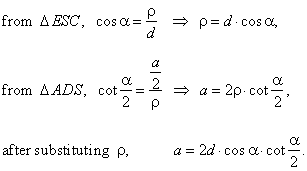| Example:
Given is the sum a +
b of legs and the angle
a of a right triangle. Find its hypotenuse
c and the sides,
a
and b,
see the figure below. |
| Solution: Given
a + b
and a.
a,
b
and c
= ? |
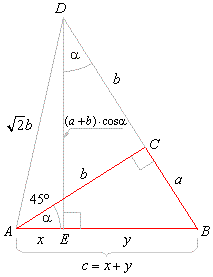
| From
D
ADE, |
 |
|
 |
|
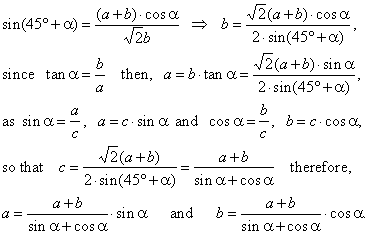| The hypotenuse can also be
calculated as c =
x + y. |
|
|
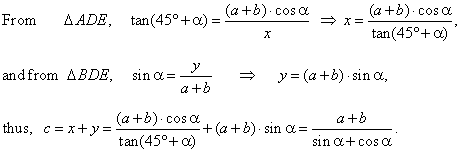
| Example:
From a distance an observer sees the top of a church tower at the angle of elevation a =
18°9′34″
when comes 100 m closer, under the angle
b
= 28°39′50″. Find the height
h
of the church and
the distance x. |
| Solution: From the
two right triangles |
|
|
|
|
| Example:
Find the angle a
between a lateral edge and the base, and the base-to-face dihedral angle
b of the regular tetrahedron shown in
the figure below. |
| Solution: R -the radius of circumscribed circle,
r
-the radius of inscribed circle, h
-height of the tetrahedron and ha -height of a face
(the equilateral triangle). |
|
|
|
|
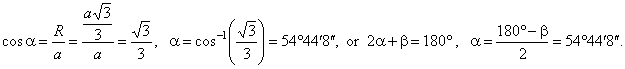
| Example:
The base of a right prism is the right-angular triangle with hypotenuse
c
and the angle a. |
| The
prism is intersected by the plane passing through the hypotenuse of the lower base and the vertex of the right
angle of the upper base and so with the base forms the angle
b, as shown in
the below figure. |
| Determine the volume of
the pyramid cut off from the prism? |
| Solution: Given
c,
a
and b.
V
= ? |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
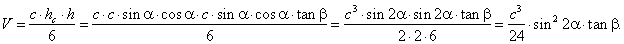
| Geometry
and use of trigonometry contents - B |
|
|
 |
|
| Copyright
© 2004 - 2020, Nabla Ltd. All rights reserved. |
