|
| Geometry - solid figures
solved problems |
|
|
|
Solid figures, solved problems examples |
|
|
|
|
|
|
| Example:
A right triangle with legs a
and b
and the hypotenuse c
first rotates around the leg a
and then around the leg b.
Find the ratio of volumes of generated solids of revolution. |
| Solution: Given a
and b.
Vs.r.
- a
: Vs.r.
- b
= ? |
|
|
| Example:
Sides of a triangle are 34,
20
and 18
cm long. Find the volume of a solid generated by rotation
of
the triangle
around a line passing through the vertex opposite of triangles' longest side and which is parallel to
it. |
| Solution: Given
a
= 34 cm, b
= 20 cm
and c
= 18 cm. Vs.r.
= ? |
|
|
 |
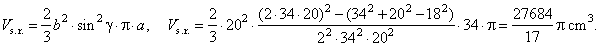| Example:
A triangle with sides 5,
4
and 3
cm, rotates around the longest side, find the volume of the solid
of revolution. |
| Solution: Given
a
= 5, b
= 4 and c
= 3. Vs.r.
= ? |
|
|
 |
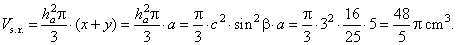| Example:
An isosceles trapezium with longer base 9
cm, shorter base
5 cm
and with leg 3
cm rotates around shorter base.
Find the volume of the solid of revolution. |
| Solution: Given
a
= 9
cm, c
= 5 cm and b
= 3 cm. Vs.r.
= ? |
|
|
| Example:
An isosceles trapezium with longer base 9 cm, shorter base
1 cm
and with leg 5 cm
rotates around longer base.
Find the surface of the solid of revolution. |
| Solution: Given
a
= 9
cm, c
= 1 cm and b
= 5 cm. Ss.r.
= ? |
|
|
| Example:
A rhombus with longer diagonal f
and shorter diagonal e
rotates around the shorter diagonal. If (
f
/
6 )2
= 1/e, find the volume of the generated solid of revolution.
|
| Solution: Given
(
f
/
6 )2
= 1/e.
Vs.r.
= ? |
|
|
| Example:
An isosceles triangle of the base a
and the leg b, rotates around the base
a. If the altitude to the
base a
is twice the length of the altitude to the leg b, find the surface of the solid of revolution. |
| Solution: Given
a and
ha
= 2hb.
Ss.r.
= ? |
|
|
| Example:
Find the surface of a regular hexagonal pyramid whose height is four times longer than the altitude of any of six
equilateral triangles that form hexagonal base. |
| Solution: Given
h1
and h
= 4h1.
S
= ? |
|
|
|
|
|
|
|
|
|
|
|
|
|
| Geometry
and use of trigonometry contents - B |
|
|
 |
|
| Copyright
© 2004 - 2020, Nabla Ltd. All rights reserved. |
