Power series
      Power series or polynomial with infinitely many terms
         The sum of a power series is a function
      Maclaurin and Taylor series
         The radius of convergence or the interval of convergence
Power series or polynomial with infinitely many terms
A real power series in x around the origin (or centered at the origin) is a series of functions of the form 
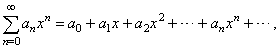and the power series around a given point x = x0 (or centered at x0) is a series of the form 
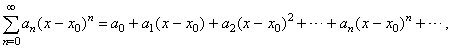where the coefficients an are fixed real numbers and x is a real variable.
A power series with real coefficients is said to be real or complex according as both x and x0 are real or complex numbers.
Therefore, the nth partial sum of a power series is a polynomial of degree n,
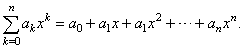The sum of a power series is a function
The sum of a power series is a function
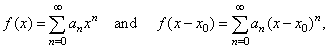the domain of which is the set of those values of x for which the series converges to the value of the function.
Maclaurin and Taylor series
Consider the polynomial function
f(x) = anxn + an - 1xn - - 1 + · · · +  a3x3 + a2x2 + a1x + a0.
If we write the value of the function and the values of its successive derivatives, at the origin, then
f(0) = a0,     f '(0) = 1· a1,     f ''(0) = 1· 2a2,     f '''(0) = 1· 2· 3a3,  . . .  ,  f (n)(0) = n!an  
so we get the coefficients;
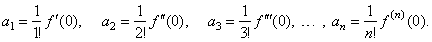Then, the polynomial f(x) with infinitely many terms, written as the power series
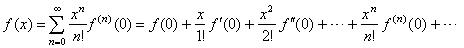and
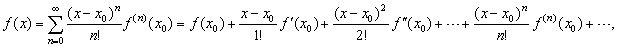where 0! = 1,   f (0)(x0) =  f(x0) and  f (n)(x0) is the nth derivative of  f at x0,
represents an infinitely differentiable function and is called Maclaurin series and Taylor series respectively.
The radius of convergence or the interval of convergence
  - If the power series  anxn  converges when x = x1, then it converges for every x that is closer to the
    origin than x1, that is, whenever  | x | < | x1 |.
  - If the power series  anxn  diverges when x = x1, then it diverges for every x that is further from the origin
    than x1, that is, whenever  | x | > | x1 |.
The real power series converges for all absolute value of x that are less than a number r, called the radius of convergence or the interval of convergence, written  | x | < r  that is, the open interval  - r < x < r.
We apply the root test or the ratio test to find the interval of convergence. Thus,
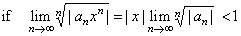  the power series 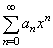converges,
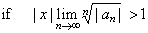    the power series diverges.  
Therefore the inequality,
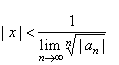defines the interval in which the power series is absolutely convergent.
Thus, denoting the right side of the above inequality by r, we get the interval of convergence | x | < r saying, for every x between  - r and r  the series converges absolutely while, for every x outside that interval the series diverges.
Therefore, the radius of convergence of the power series,
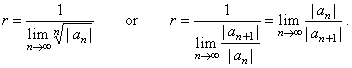The power series  anxn  converges absolutely at every point x from the open interval  - r < x < r and diverges for all x outside this interval. At the endpoints  - r and r, the series may converge or diverge so these points must be checked for convergence, individually.
The power series  an(x - x0)n  converges absolutely at every point x from the open interval |x - x0| < r or
x0 - r < x < x0 + r   and diverges for all x outside this interval.
Note that the series may or may not converge when | x - x0 | = r that is, when  x = x0 - r  or  x = x0 + r.
To determine whether the power series converge or diverge at endpoints we should plug each endpoint into the given series and apply appropriate test for convergence.
Functions contents E
Copyright © 2004 - 2020, Nabla Ltd.  All rights reserved.