|
|
|
Power
series
|
 Power
series or polynomial with infinitely many terms
Power
series or polynomial with infinitely many terms |
|
The
sum of a power series is a function |
 Maclaurin and Taylor series
Maclaurin and Taylor series |
|
Representing
polynomial using Maclaurin's and Taylor's formula |
|
Representing
polynomial using Maclaurin's and Taylor's formula, examples |
|
|
|
|
|
|
| Power
series or polynomial with infinitely many terms |
| A
real power series in x
around the origin (or centered at the origin) is a series of functions of the form |
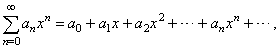 |
| and
the power series around a given point x
= x0 (or centered
at x0)
is a series of the form |
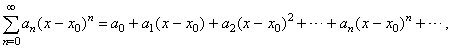 |
| where
the coefficients an
are fixed real numbers and x
is a real variable. |
| A
power series with real coefficients is said to be real or complex
according as both x
and x0
are real or complex
numbers. |
| Therefore,
the nth
partial sum of a power series is a polynomial of degree n, |
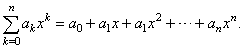 |
|
| The
sum of a power series is a function |
| The
sum of a power series is a function |
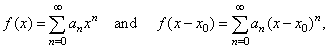 |
| the domain of
which
is the set of those values of x
for which the series converges to the value of the function. |
|
| Maclaurin and Taylor series |
| Consider
the polynomial function |
|
f (x) = anxn
+ an -
1xn -
-
1 + · · · + a3x3
+ a2x2 + a1x
+ a0.
|
| If
we write the value of the function and the values of its successive
derivatives, at the origin, then |
| f
(0) =
a0, f '(0) = 1· a1,
f ''(0) = 1· 2a2,
f '''(0) = 1· 2· 3a3, . . .
, f (n)(0) =
n!an |
| so we
get the coefficients; |
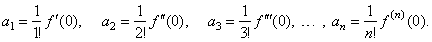 |
|
| Then,
the polynomial
f (x)
with infinitely many terms, written as the power series |
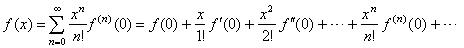 |
and |
|
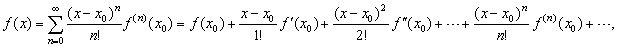 |
| where
0! = 1,
f (0)(x0)
= f
(x0)
and
f (n)(x0)
is the nth
derivative of f at
x0, |
|
represents an infinitely differentiable function
and is called Maclaurin series and Taylor series respectively. |
|
| Representing
polynomial using Maclaurin's and Taylor's formula |
| If
given is an n-th
degree polynomial |
| Pn
(x) =
an xn + an -
1xn -1 + ·
· · + a2
x2
+ a1 x + a0 then, |
| Pn(0) =
a0,
Pn' (0) = a1,
Pn''(0) = 2!
a2,
Pn'''(0) = 3!
a3,
. . . , Pn(n)(0) = n!
an
and
Pn(n
+ 1) = 0 |
| so,
the coefficients of the polynomial |
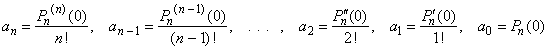 |
| therefore,
applying Maclaurin's formula, every polynomial can be written as |
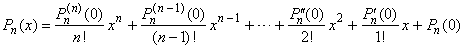 |
| since
Pn(n
+ 1) = 0,
the remainder vanishes. |
|
| Example: Represent
the quintic y
= 2x5 + 3x4 -
5x3 + 8x2 -
9x + 1 using Maclaurin's
formula. |
| Solution: Let write
all successive derivatives of the given quintic function and evaluate them at the
origin, |
|
y' (x)
= 10x4 + 12x3 -
15x2 + 16x -
9,
y' (0)
= -
9 |
|
y'' (x)
= 40x3 + 36x2 -
30x + 16,
y'' (0)
= 16 |
|
y''' (x)
= 120x2 + 72x -
30,
y''' (0)
= -
30 |
|
yIV
(x)
= 240x + 72,
yIV
(0)
= 72 |
|
yV
(x)
= 240,
yV
(0)
= 240 |
|
yVI
= 0 and the last term of the polynomial a0
= y(0)
= P5(0) =
1, |
| then
substitute obtained values into Maclaurin's
formula |
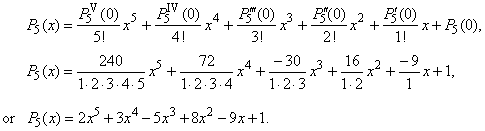 |
|
| Example: Represent
the quartic y
= x4 -
4x3 + 4x2 + x -
4 at x0
= 2 using
Taylor's
formula. |
| Solution: Let write
all successive derivatives of the given quartic and evaluate them at x0
= 2, |
|
y' (x)
= 4x3 -
12x2 + 8x + 1,
y' (2)
= 1 |
|
y'' (x)
= 12x2 -
24x + 8,
y'' (2)
= 8 |
|
y''' (x)
= 24x -
24,
y''' (2)
= 24 |
|
yIV
(x)
= 24,
yIV
= 24 |
|
yV
(x)
= 0
and the last term, a0
=
y(2)
= P4(2) = -
2, |
| then
substitute obtained values into Taylor's
formula |
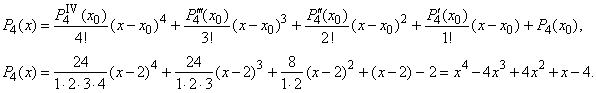 |