|
|
Series |
|
Absolute
convergence |
|
Conditional
convergence |
 Series
of positive terms
Series
of positive terms |
|
|
|
|
|
|
|
| Absolute
convergence of a series |
| An
infinite series |
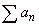 |
is called absolutely convergent if the infinite series |
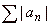 |
is convergent, i.e., |
|
|
the series
of absolute values of its
terms converge. |
| Thus,
if a series is absolutely convergent, then both series, |
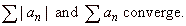 |
|
|
| Example: Let
show that the series |
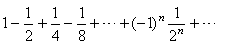 |
is
absolutely convergent. |
|
| Solution: Given
series is absolutely
convergent since the series
of absolute values of its
terms |
| |
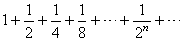 |
converges
to 2, |
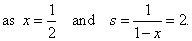 |
|
|
| Therefore,
the series |
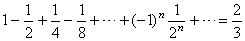 |
is
convergent and its sum is 2/3. |
|
|
| Example: Let
show that the series |
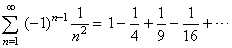 |
is
absolutely convergent. |
|
| Solution: Given
series is absolutely
convergent since the series
of absolute values of its
terms |
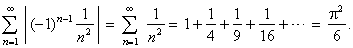 |
| Therefore,
the series converges and its sum |
 |
|
|
| Conditional
convergence |
| If
an infinite series |
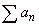 |
is not convergent, it is called divergent. However, if it is convergent
but not |
|
|
absolutely convergent,
it is called conditionally convergent. |
|
| Series
of positive terms |
| Suppose
the series |
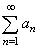 |
consists
of positive terms only. Then its partial sums |
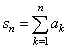 |
form
an |
|
| increasing sequence, therefore given series converges if and only if
the sequence of partial sums {sn}
is |
| bounded. |
|
We use this property for convergence tests of series with positive
terms. |
|
| Example: The series of positive terms |
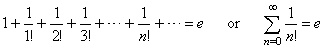 |
| converges
since |
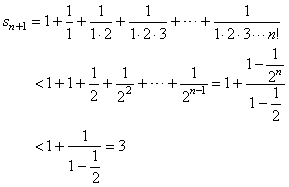 |
| that
is, the sequence of partial sums is
bounded above, and the series converges to the number e. |
| If
we calculate the partial sum of first 10 terms of the series,
s10
= 2.718281
obtained
is the number e
to six
correct
decimal digits
what shows that the series
increases relatively fast. |
|