|
|
Series |
 Alternating
series
Alternating
series |
|
Alternating series test
or Leibnitz's
alternating series test |
|
|
|
|
|
|
|
| Alternating
series |
| A
series the terms of which are alternately positive and negative is
called the alternating series. |
| Alternating series test
or Leibnitz's
alternating series test |
| An
alternating series converge if the absolute values of its terms decrease
monotonically to zero as n
tends to
infinity. |
| Given
an alternating series a1
-
a2 + a3 -
+
·
·
·
+
(-1)n
-
1
an +
·
·
· |
| suppose
a1
> a2 > a3 > ·
·
·
> an
> an
+ 1 > ·
·
·
> 0
and |
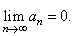 |
|
| The
sequence of the partial sums sn
of the series alternate approaching the same limit s.
The terms of s2n
of the
even
indices,
increase while the terms of s2n
+ 1 of the odd indices,
decrease as is shown on the number line
below. Every term of the sequence of an even index is smaller than every
term of an odd index therefore, s2n
< s
< s2n
+ 1 |
 |
| and |
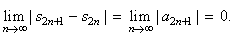 |
|
|
|
| Example: Let
show that the series |
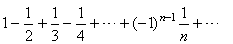 |
converges. |
|
| Solution: The
given alternating series converges since the sequence of absolute values of its
terms |
| |
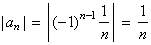 |
that
is, |
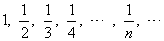 |
|
|
| decrease to zero as
n
tends to infinity, or |
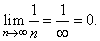 |
The
series converges to ln
2 or s
= ln 2. |
|
| Note
that the given logarithmic series is not absolutely convergent since |
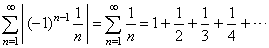 |
| obtained
harmonic series diverges. |
| Therefore,
the series |
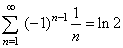 |
is
said to be conditionally convergent. |
|
|
| Example: Let
show that the series |
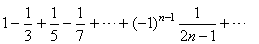 |
converges. |
|
| Solution: The
given alternating series converges since the sequence of absolute values of its
terms |
| |
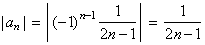 |
that
is, |
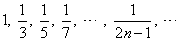 |
|
|
| decrease to zero as
n
tends to infinity, or |
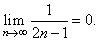 |
As
Leibnitz proved, the
series converges to p/4. |
|
|