|
|
|
Series |
 Infinite series
Infinite series |
|
The sequence of partial
sums |
|
The
sum of the series |
|
Convergence
of infinite series |
|
Divergence
of infinite series |
|
Convergent
and divergent series
examples |
|
|
|
|
|
|
| Infinite series |
| An
infinite series is the sum of infinite sequence of terms which we
denote |
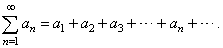 |
| That
is, given an infinite sequence of real numbers, a1,
a2, a3, . . . , an,
. . .
all of the terms of which are added
together, where an
denotes the general term of the series. |
|
| The
sequence of partial
sums |
| Recall
that we've already dealt with infinite series in previous section when
representing real numbers as infinite
decimals. Thus, for example the real number |
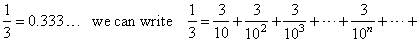 |
| so,
when adding up this infinite number of terms, we start by calculating
its partial sums |
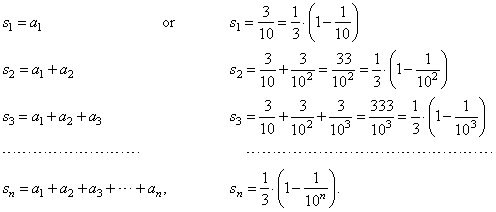 |
| Thus,
obtained is sequence {sn}
of the partial sums, s1,
s2, s3, . . . , sn,
. . .
where sn
denotes the sum of
the first n
terms of the series and is called the nth
partial sum. |
| Therefore,
the
limit of the sequence {sn}
as n
tends to infinity, i.e., |
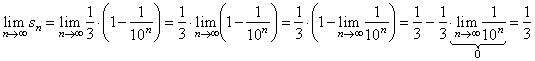 |
|
equals the value of the real number 0.333
. . .
that is, equals the sum of
the infinite series. |
|
|
The
sum of the series |
| An infinite series has a sum if the sequence of its partial sums
converge to a finite number s,
i.e., |
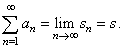 |
| The sum of
an infinite series is the limit of its partial sums
as n
tends to infinity. |
| Let
rewrite the above example using this notation, |
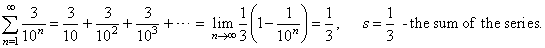 |
| where, |
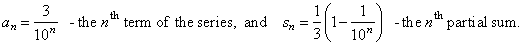 |
|
|
| Convergence
of infinite series |
| If
the
limit of the sequence of partial sums
exists
as a real number, then the series is convergent. |
|
| Divergence
of infinite series |
| If
the limit of the sequence of partial sums does not exist or tends
to +
oo
or -
oo, |
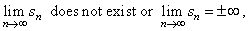 |
| then, the series is
divergent or oscillates. |
|
| Convergent
and divergent series
examples |
| Example: Show
that the series |
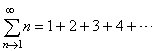 |
diverges. |
|
| Solution:
The given
infinite sum of natural numbers is called the arithmetic series. |
| Using
the formula for the sum
of the arithmetic sequence, whose difference d
= 1,
we calculate the sum of the first n
terms of the series. |
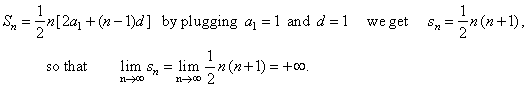 |
|
| Example: Let
show
that the series |
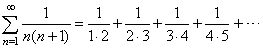 |
converges. |
|
| Solution:
We
use the method of partial
fraction decomposition to rearrange given expression. |
| Since
the denominator consists of linear factors then, we can write |
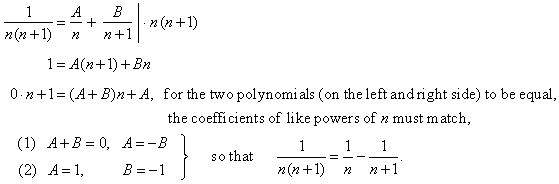 |
| Therefore, |
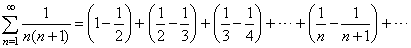 |
|
| Since
the second and the first term of any two successive parentheses cancel
then,
the sum of
the first n
terms of the series |
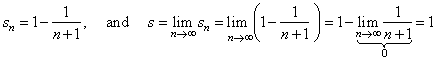 |
|
therefore the series converge, and its sum s
= 1. |
|
| Example: Show
that the series |
 |
converges. |
|
| Solution:
Use the method of partial
fraction decomposition to rearrange given expression. |
| Since
the
number of the coefficients used in the expansion relates to the degree
of the polynomial in the denominator,
and as it consists of linear factors some of which are repeated
then, |
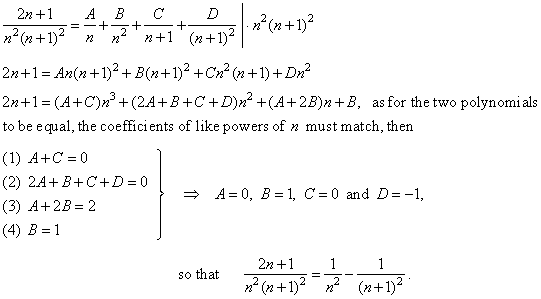 |
| Therefore, |
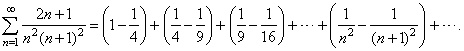 |
|
| Since
the second and the first term of any two successive parentheses cancel
then, the sum
of
the first n
terms of the series |
|
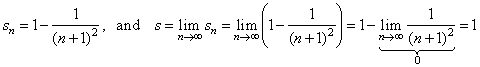 |
|
therefore the series converge, and its sum s
= 1. |
|
|
|
|
|
|