|
|
|
|
The limit of a sequence
theorems |
Some
important limits |
|
Operations
with limits |
|
Operations
with limits examples |
|
|
|
|
|
|
|
| Some
important limits |
| (1)
Let examine convergence of the sequence given by an
= | a |n |
|
a) if | a |
> 1 then we can write |
a | = 1 + h,
where h
is a positive number. |
| So,
by the binomial theorem |
 |
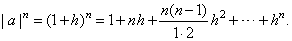| If
we drop all terms beginning from the third that are all positive since
the binomial coefficients are natural numbers, if n > 2
and h
> 0, the right side become smaller, so obtained is the Bernoulli's
inequality |
| (1 + h)n
> 1 + nh,
n > 2. |
| When
n
®
oo
then 1 + nh
tends to the positive infinity too, since we can make 1 +
nh
greater than any |
| given positive number N,
if only we take |
 |
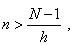therefore will even more tend to infinity
| a |n
which is |
|
| greater.
Thus, |
 |
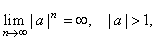or |
 |
|
|
|
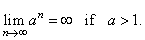| b) if
0 < | a | < 1 then we can write |
 |
|
|
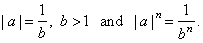| Since b
> 1 then |
 |
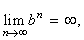such that | a |n
< e
whenever |
 |
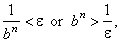however small e is, |
|
| this
inequality can be satisfied by choosing n
large enough. Therefore, |
 |
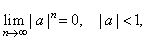or |
 |
|
|
|
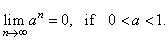| (2) Let examine convergence of the sequence given by |
 |
|
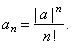| The
sequence |
 |
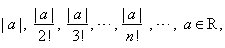the n-th
term of which we can write as |
|
 |
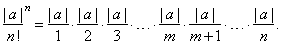| For
every | a | >
1 there exists a natural number m
such that m <
| a | < m + 1
and n
> m
then |
 |
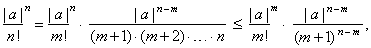| since |
 |
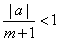it follows that an
® 0
or we write |
|
|
|
|
| (3) Let examine convergence of the sequence given by |
 |
|
|
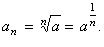a) If a
> 1 then the sequence |
 |
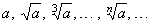is decreasing, that is |
|
 |
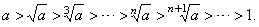| Let |
 |
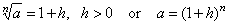then by the Bernoulli's
inequality a
> 1 + nh
so that |
|
 |
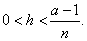Since the numerator a
-
1 is fixed number then,
if n ® 0
then h ® 0
too, therefore |
|
 |
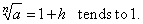So we
can write |
 |
|
|
|
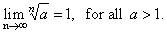b) If
0 < a < 1 then the sequence |
|
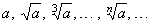is increasing, that is |
|
 |
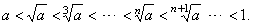| For
example, |
 |
|
|
|
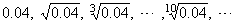| If
we write |
 |
|
 |
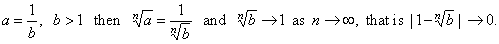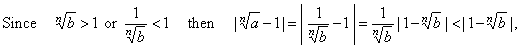| so it
follows that |
 |
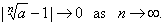Therefore,
|
 |
|
|
|
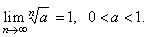c) If
a = 1 then |
 |
|
|
|
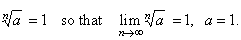| Since
in all three cases above, a), b) and c) we've got the same result,
then we can write |
|
|
|
|
