|
|
|
Series |
Infinite
series |
|
Harmonic
series |
|
|
|
|
|
|
| Infinite series |
| An
infinite series is the sum of infinite sequence of terms which we
denote |
 |
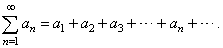| That
is, given an infinite sequence of real numbers, a1,
a2, a3, . . . , an,
. . .
all of the terms of which are added
together, where an
denotes the general term of the series. |
|
| Harmonic
series |
| The
series of the reciprocals of natural numbers |
 |
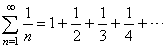| is
called the harmonic series since the middle term of any three successive
terms is the harmonic mean of the
other two. |
| Given
three positive numbers, a,
b
and c
are said to be in the harmonic proportion if |
 |
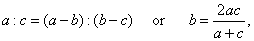| that
is, if b
is the harmonic mean of the numbers, a
and c. |
| Therefore,
any three successive terms, |
 |
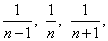of
the harmonic series, are in the harmonic |
|
| proportion since |
 |
|
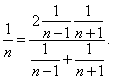| As,
in the harmonic proportion a
> c then, a
-
b > b -
c therefore a
+ b > 3b -
c |
| or
a
+ b + c > 3b. |
| That
is, the sum of any three successive terms of the harmonic series is
three times greater than the middle term.
P. Mengoli (1626 - 1686) used this property to prove divergence of the
harmonic series. |
| Let
examine behavior of the sequence of partial sums of the harmonic series
applying this property. |
| Thus,
the sum of the three successive terms beginning from the second gives |
 |
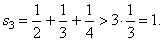| Next
nine terms, from n = 5 to
13, divide in three groups with three terms in
each, so that; first gives |
|
|
| Therefore, |
 |
|
|
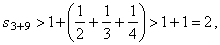| since
the parentheses
equals already known value s3. |
| For
next 27
terms, from n =
14 to 40,
following the same procedure, we get that their sum is greater
than |
| |
 |
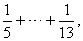for
which is already shown that is >
1,
thus s3 +
9 + 27
> 3. |
|
|
| Generally,
it can be written |
 |
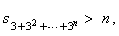that
is, the partial sums sn increase
to infinity as n
®
oo. |
|
| Therefore,
the harmonic series diverges. |
|
|
|
|
|
|
