|
|
|
Quadratic Equations and Quadratic
Function |
 Graphing a quadratic
function
Graphing a quadratic
function |
|
Transformations
of the graph of the quadratic function |
| |
|
|
|
|
|
| Graphing a quadratic
function |
| Transformations
of the graph of the quadratic function |
| How
changes in the expression of the quadratic function affect its
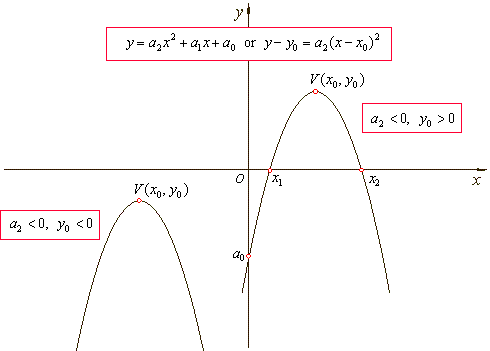
graph is shown in the figures below. |
|
|
|
|
 |
|
The graph of quadratic polynomial will intersect the
x-axis in two
distinct points if its leading coefficient a2
and the vertical translation
y0
have different signs, i.e., if a2
· y0
<
0. |
|
|
| Example:
Find zeros and vertex of
the quadratic function y
=
-
x2
+ 2x
+
3
and sketch its graph. |
| Solution:
A quadratic function can
be rewritten into translatable form y
-
y0
= a2(x
-
x0)2
by completing the square, |
|
y
=
-
x2
+ 2x
+ 3 |
Since a2
· y0
<
0 given
quadratic function must have two different real zeros. |
|
y
=
-
(x2
-
2x)
+ 3 |
To find zeros of a function, we set
y
equal to zero and solve for x.
Thus, |
|
y
=
-
[(x
-
1)2
-
1]
+ 3 |
-
4
=
-
(x
-
1)2 |
| y -
4
=
-
(x
-
1)2 |
(x
-
1)2
=
4 |
| y
-
y0
= a2(x
-
x0)2 |
x
-
1
=
±
sqrt(4) |
| V(x0,
y0)
=>
V(1,
4) |
x1,2
=
1
±
2, =>
x1
= -
1
and x2
= 3. |
|
 |
| We
can deal with the given quadratic using the property of the
polynomial explored under the title, |
| '
Source
or original polynomial function '. Thus, |
| 1)
calculate the coordinates of translations of the quadratic
y
=
f (x) =
-
x2
+ 2x
+
3 |
|
|
| 2)
To
get the source quadratic function, plug the coordinates
of translations (with changed signs)
into the general form
of the quadratic, i.e., |
| y
+ y0
= a2(x
+ x0)2
+ a1(x
+ x0)
+ a0
=> y
+ 4
= -
(x
+ 1)2
+ 2(x
+ 1)
+
3 |
|
y
=
-
x2
the source quadratic function |
| 3)
Inversely, by plugging the coordinates of translations into the source quadratic function |
| y
- y0
= a2(x
- x0)2
=> y
- 4
= -
(x -
1)2
|
|
obtained is given quadratic in general form
y
=
-
x2
+ 2x
+
3. |
|
|
|
|
|
|
|
|
|
|
|
| Functions
contents A |
|
 |
|
| Copyright
© 2004 - 2020, Nabla Ltd. All rights reserved. |