|
|
|
Binomial
equations |
 Solving binomial equations
Solving binomial equations |
|
Equations
reducible to quadratic - biquadratic equations |
 Solving equations reducible to quadratic
Solving equations reducible to quadratic |
|
|
|
|
|
|
| Binomial
equations |
| An
equation of the form axn
±
b
=
0, a
> 0, b > 0 and n is a natural number is
called the binomial equation. |
|
| Solving binomial equations |
| By using
substitution |
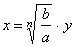 |
the
equation transforms to |
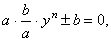 |
or |
y
n
±
1
=
0. |
|
|
| Recall
that the expression on the left side can be factorized, for example: |
|
y3 +
1
=
(y + 1) · (y2 -
y
+ 1) |
|
y3 -
1
=
(y -
1) · (y2 +
y
+ 1) |
|
y4 +
1
=
(y2
+ 1)2 -
2y2
=
(y2
+ 1 -Ö2
y)
· (y2
+ 1 + Ö2
y) |
|
y4 -
1
=
(y2
-
1) · (y2 +
1)
=
(y -
1) · (y + 1) · (y2 +
1) |
|
y5
+
1
=
(y +
1) · (y4 -
y3 +
y2 -
y
+
1) |
|
y5
-
1
=
(y -
1) · (y4 +
y3 +
y2 +
y
+
1) |
|
y6
-
1
=
( y3 -
1)
· (y3 +
1)
=
(y -
1) · (y + 1) · (y2 +
y
+ 1) · (y2 -
y
+ 1) and so on. |
|
| Example:
Solve the binomial
equation
8x3
-
27 =
0. |
| Solution:
Let substitute |
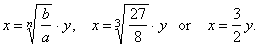 |
|
|
|
|
|
| To obtain the values of the
original variable plug the solutions into the substitution
x =
(3/2)y |
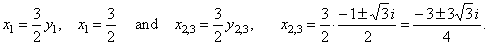 |
|
| Example:
Solve the binomial
equation
x4
+ 81
=
0. |
| Solution:
By substituting |
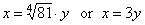 |
obtained
is |
|
|
|
|
| To obtain the values of the
original variable plug the solutions into the substitution
x =
3y |
|
|
|
|
Equations
reducible to quadratic form - biquadratic equations |
| A
bi-quadratic equation is said to be reducible to quadratic if the variable
factor of the leading term is the square of the variable factor
in the middle term. |
| Solving bi-quadratic
equations or equations reducible to quadratic |
|
Thus, a biquadratic equation |
| ax4
+
bx2
+
c
=
0 we can
write a(x2)2
+
bx2
+
c
=
0 |
| and
solve as the quadratic equation in the unknown
x2
using the substitution x2
=
y. |
|
| Example:
Solve the biquadratic
equation 3x4
-
4x2
+ 1
=
0. |
| Solution:
By substituting x2
=
y we get the quadratic equation |
| 3y2
-
4y
+ 1
=
0 |
|
|
| To obtain the values of the
original variable plug the solutions into the substitution
x2
=
y |
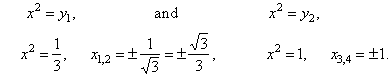 |
|
| An
equation of the form ax2n
+
bxn
+
c
=
0,
where
n is a natural
number greater than 2, we can reduce to quadratic
using the substitution xn
=
y. |
| So,
obtained is the quadratic equation ay2
+
by
+
c
=
0 the solutions
of which are, y1
and y2. |
| Then,
to obtain the values of the
original variable, we plug the solutions into the substitution
xn
=
y. |
| Therefore,
xn
=
y1 and
xn
=
y2
are the two binomial equations |
| xn
-
y1
=
0 and
xn
-
y2
=
0 |
| that
have 2n
solutions. |
|
| Example:
Solve the equation
x6
-
7x3 -
8 =
0 that is
reducible to quadratic form. |
| Solution:
By substituting x3
=
y we get the quadratic equation |
| y2
-
7y -
8 =
0 |
|
|
| To obtain the values of the
original variable plug the solutions into the substitution
x3 =
y |
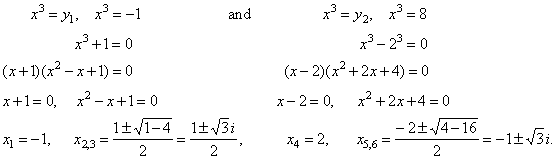 |
|
|
|
|
|
|
|
|
|
|
|
| Functions
contents A |
|
 |
|
| Copyright
© 2004 - 2020, Nabla Ltd. All rights reserved. |