|
|
Applications
of differentiation - the graph of a function and its derivatives |
 Points
of inflection
Points
of inflection |
|
Points
of inflection and concavity of the sine function |
|
Points
of inflection and concavity of the cubic polynomial |
|
|
|
|
|
|
| Points
of inflection |
| The
point of the graph of a function at which the graph crosses its tangent
and concavity changes from up to down
or vice versa is called the point of inflection. |
| Therefore, at
the point of inflection the second derivative of the function is zero and changes its sign. |
|
| Points
of inflection and concavity of the sine function |
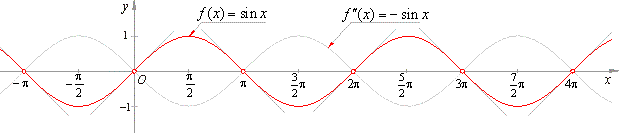
| For
example, the graph of f
(x)
= sin x
is concave
up inside the intervals |
|
(2k -
1)p
< x < 2kp,
k = 0,
+1,
+2,
. . .
since f ''
(x) = -
sin x > 0, |
| it
is concave
down inside the intervals |
|
2kp
< x < (2k + 1)p,
k = 0,
+1,
+2,
. . .
since f ''
(x) = -
sin x < 0 |
| and
its points of inflection lie at x
= kp,
k = 0,
+1,
+2,
. . . , as shows the figure below. |
 |
| The first derivative
of a function at the point of inflection equals the slope of the tangent
at that point, so |
|
f ' (x) = cos
x
thus, m
=
f
' (kp)
= cos (kp)
= ±1,
k = 0,
+1,
+2,
. . . |
|
| Point
of inflection and concavity of the cubic polynomial |
| Let
examine concavity of graphs of cubic polynomial f (x) = a3x3 + a2x2
+ a1x + a0 . |
| The
coefficient a1
of the source cubic defines three types of cubic functions. |
| To obtain
the source form
we should plug the coordinates of translations |
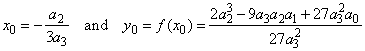 |
|
into y
+ y0 = a3(x
+ x0)3
+ a2(x + x0)2
+ a1(x + x0)
+ a0,
so we get |
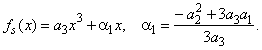 |
| To
find the abscissa of the point of inflection of the cubic polynomial we
should solve f ''
(x) = 0
for x, |
|
since f
' (x) = 3a3x2 + 2a2x
+ a1 |
|
then f ''
(x) = 6a3x + 2a2,
so that f ''
(x) = 0
gives
x = -
a2
/ (3a3)
= x0 . |
| Therefore,
the
abscissa of the point of inflection coincide
with the translation of the cubic in direction of the
x-axis.
Since
the first derivative
of a function at the point of inflection equals the slope of the tangent
at that point,
then |
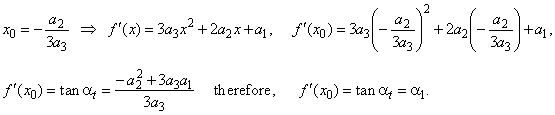 |
| Thus,
the value of tan at
= a1
defines the three types of cubic functions as is shown in the figure
below. |
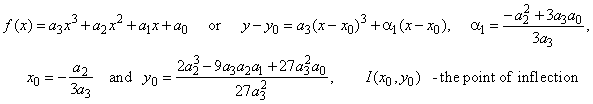 |
| type
1 )
y
-
y0 = a3(x
-
x0)3 |
and type
2 )
and
3 )
y -
y0 = a3(x
-
x0)3
+ a1(x
-
x0) |
|
| 1
)
tan at
= a1
= 0 |
2
)
tan at
= a1
> 0 |
3
)
tan at
= a1
< 0 |
|
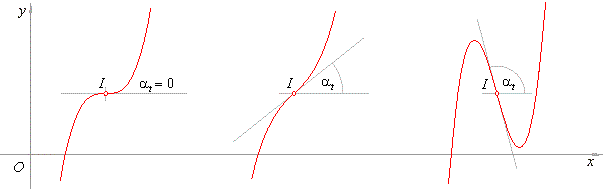 |
| Note
that all three graphs are drawn assuming a3
> 0. |
|
|
|
|