|
|
Applications
of differentiation - the graph of a function and its derivatives |
 Approximate
solution to an equation, Newton's method (or the Newton-Raphson method)
Approximate
solution to an equation, Newton's method (or the Newton-Raphson method) |
|
Use of
Newton's method, example |
|
|
|
|
|
|
|
| Approximate
solution to an equation, Newton's method (or the Newton-Raphson method) |
| The
mean value theorem can be applied to find approximate value of a root of
a function. |
| Newton's
method is iterative method to approximate solution
to
the equation f (x) = 0
to
a desired accuracy. |
| If
a
function f
continuous on the closed
interval [a,
b]
satisfies
following conditions, |
| -
its function values at endpoints of the interval are of the opposite
signs |
| -
the
first and second derivatives of which do not change the sign on the
interval,
f
' (x)
and f ''
(x)
is not
0 |
| then,
we can find approximate value of the root of the function within the
interval [a,
b]
using Newton's method. |
| Since
f
' (x)
is not
0,
the graph of f
intersects
the x-axis
only once at the root of the function,
and because of f ''
(x)
is not
0
corresponding
arc
AB
is concave up or concave down within
the interval. |
| Newton's
method begins
by drawing the line tangent to the graph at the endpoint of the interval
at which f (x)
· f ''
(x) > 0
taking the intercept of the tangent with the x-axis
as the approximate value of
the root of the
function. |
| Thus,
each of two signs of the second derivative, f ''
(x) > 0
or f ''
(x) < 0
determines two cases, depending
whether
f
' (x) > 0
or f
' (x) < 0,
there are four possible cases as shows the figure below. |
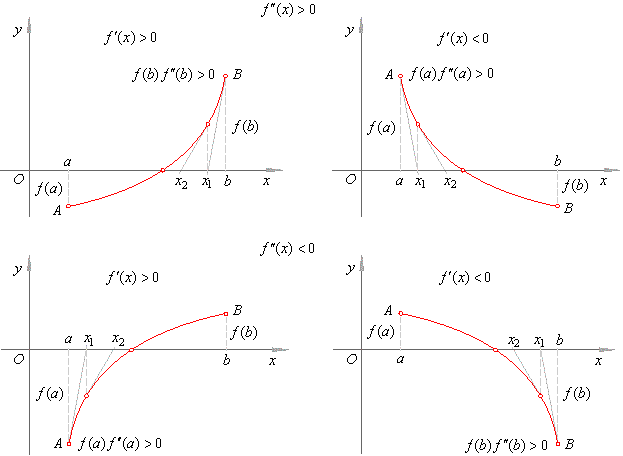 |
| Note
that, by satisfying f (x)
· f ''
(x) > 0
in each of four cases the intercept x1
is closer approximate value
of
the root than x = a
or x = b. |
| The
x-intercept
of the tangent |
| y
= f (b) + f
' (b)
(x -
b) |
| at
the point B
of the curve, we get by solving y
= 0
for x, |
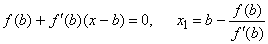 |
| where,
x1
is the
approximate value of
the root. |
| If
the function value f (x1)
does not satisfy required accuracy then the same process can be
repeated at (x1, f (x1)) and
so on until a predetermined level of accuracy is reached, |
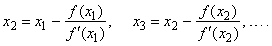 |
| Therefore,
Newton's method generates a sequence of approximations x1,
x2,
x3,
x4,
. . . , until reached is desired level of accuracy.
If
we have found xn,
the next approximation is
the solution of the equation |
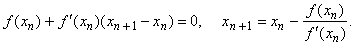 |
|
| Use
of Newton's method example |
| Example:
Use
Newton's method to approximate the root of the function
f (x) = x4
-
4x3 + 4x2 + x -
4, located
within the interval [2,
3], with an error
less than 0.0001. |
| Solution:
Let's first chose the starting point x
that satisfies the necessary condition f (x)
· f ''
(x) > 0
to ensure
the use of
Newton's method the right way. |
| Since
f
' (x) = 4x3
-
12x2 + 8x + 1
and f
'' (x) = 12x2
-
24x + 8, |
| by
plugging the endpoints x =
2
and x =
3
of the given interval into f (x)
and f
'' (x) we
get, |
|
f (2) =
-
2
and f
'' (2) = 8
so that f (2)
· f ''
(2)
< 0
therefore, x =
2
fail |
| while
f (3) =
8 and f
'' (3) = 44
so that f (3)
· f ''
(3)
> 0 so we use
x0 =
3
as the
starting point. |
| We
can check the function value
f (xi)
at
each successive approximate value
xi
of the process, to estimate if
given accuracy is reached, that is, whether the xi
is close
enough to represent the root of the function. |
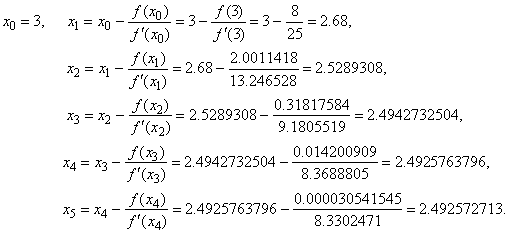 |
| The
approximate value x5 =
2.492572713
we can take as the root of the given quartic with an error
less than
10-8. |
|
|
|