|
|
|
 The
derivative as a function
The
derivative as a function |
| The
derivative function |
| Differentiation,
determining (or deriving) derivative of a function |
 Derivatives
of basic or elementary functions
Derivatives
of basic or elementary functions |
| Determining
the derivative of a function as the limit of the difference
quotient |
|
The
derivative of the power function |
|
The
derivative of the linear function
|
|
The
derivative of a constant
|
|
The
derivative of the sine function |
|
The
derivative of the cosine function |
|
|
|
|
|
|
| The
derivative as a function |
| The
derivative of a function f
(x)
is a new function that contains the value of the derivative of
all points on the original
function. |
| That is, the
derivative function gives the slope of
the line tangent to f
(x)
at every point x. |
| The
slope of the tangent line provides information about how the
graph of the function is changing. |
|
Thus,
if
f
'
(x)
<
0
then f
(x)
is decreasing |
|
and if f
'
(x)
>
0 then
f
(x)
is increasing, |
| as is shown in the
figure
below. |
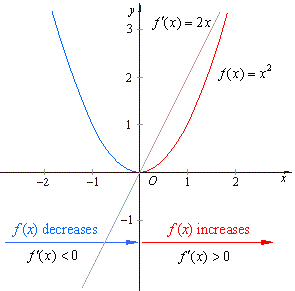
|
|
| The
process of determining or finding the derivative is called differentiation. |
| In
order a function to be differentiable, it must be continuous,
and both one-sided limits (the
left-handed and right-handed limits) must
be equal at
the given point. |
|
For example, the function f
(x)
= | x | is not differentiable
at x
= 0, although
it is continuous there. |
|
|
Derivatives
of basic or elementary functions
|
| Determining
the derivative of a function as the limit of the difference
quotient |
| We
use the limit definition |
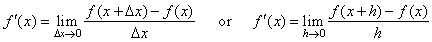 |
|
to
find the derivative of a function.
|
|
| The
derivative of the power function |
| Given
is the power function
f (x)
= xn
where n
is a a positive integer. |
|
We
use the binomial theorem to evaluate f
( x
+ h),
|
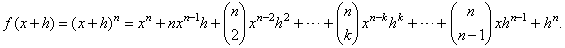 |
| So
that, f
(x
+ h) -
f (x)
equals, |
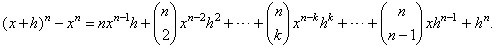 |
| Then
the difference quotient |
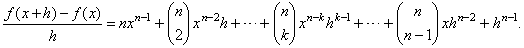 |
|
Since
every term except the first is factor of h
then,
the limit of
the difference quotient
as h
tends to zero is
|
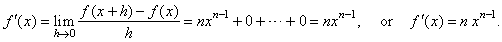 |
| |
Therefore,
if |
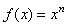 |
then |
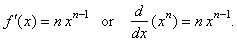 |
|
|
|
| The
derivative of the linear function
|
| Thus,
for n = 1,
that is for the linear function f
(x)
= x, the
difference
f
(x
+ h) -
f (x) = x
+ h - x
= h so that the
difference quotient equals 1.
|
| |
Therefore,
if
|
f(x)
= x |
then |
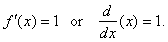 |
|
|
|
|
| The
derivative of a constant
|
| The
function f
(x)
= c,
where c
is a fixed constant, is graphically represented by a horizontal
line so that at any
given point (x,
f (x)) the slope
of the line tangent to the graph of f
is 0. Therefore, |
| f(x)
= c and
f(x
+ h)
= c
so
that f(x
+ h) -
f(x)
= c - c
= 0. |
| Thus, |
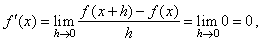
|
| |
that
is, if
|
f(x)
= c |
then |
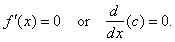 |
|
|
|
| The
derivative of the sine function |
| We
use the limit of the
difference quotient to find the
derivative of the function f
(x)
= sin x. |
|
Let
rewrite the
difference quotient applying the sum to product formula,
|
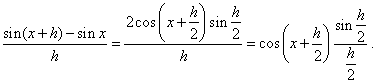 |
| Since,
the derivative is the limit of the difference quotient as h
tends to zero then, |
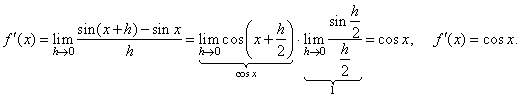 |
| |
Therefore,
if
|
f(x)
= sin x |
then |
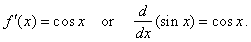 |
|
|
|
| The
derivative of the cosine function |
| We
use the limit of the
difference quotient to find the
derivative of the function f
(x)
= cos x. |
|
Let
rewrite the
difference quotient applying the sum to product formula,
|
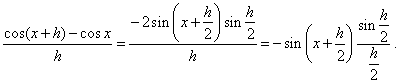 |
| Since
the derivative is the limit of the difference quotient as h
tends to zero then, |
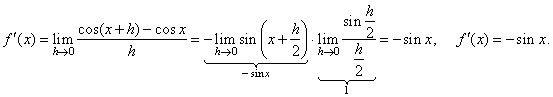 |
| |
Therefore,
if
|
f(x)
= cos x |
then |
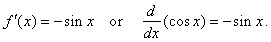 |
|
|
|
|
|
|