|
| Differential
calculus |
|
|
|
|
Differential
Calculus
- Derivatives and differentials |
Determining
the lines tangent to the graph of a function from a point outside the
function |
| Determining
the lines tangent to the graph of a function from a point outside the
function, example |
|
|
|
|
|
|
|
|
Determining the lines tangent to the graph of a function from a point outside the
function
|
|
Lines
tangent to the graph of a function y
= f (x)
from a given point (x1,
y1)
outside the function are defined
by two
points they pass through, the given point
(x1,
y1)
and the point of tangency (x0,
y0).
|
|
To
find the coordinates x0
and y0
of the points of tangency we should solve the following two
equations,
|
|
(1) y0
= f (x0) |
|
(2) y1
-
y0
= f
'
(x0) · (x1
-
x0)
|
|
as
the system of the two equations with the two unknowns x0
and y0.
|
|
The
first equation states that the point of tangency must lie on the
given function while, at the same time, its coordinates
x0
and y0
must satisfy the equation of the tangent line (2),
since the point of tangency is the common point of the
tangent
and the curve.
|
|
Thus
for example, if given is the quadratic function
f (x)
= ax2
+ bx
+ c
and
the point P1(x1,
y1)
t hen, applying
the above system of equations we can calculate
the coordinates of the points of tangency
P0
(x0,
y0)
directly from the formulas,
|
|
|
|
| Example: |
Find equations of the lines tangent
to the function f
(x)
= -
x2
+ 2x
+ 4
drawn
from the point |
|
|
(3,
2).
|
| Solution: To
find the coordinates x0
and y0
of the points of tangency we should solve the system of equations.
Substitute given quantities, the point (3,
2)
and f
(x)
= -
x2
+ 2x
+ 4
into equations, |
|
|
|
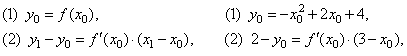
Let calculate the slope
f
'
(x0)
of the tangent line, the equation
(2).
|
|
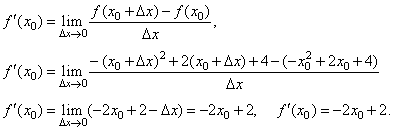
| Then
substitute the slope and the y0
into second equation to get the points of tangency, |
|
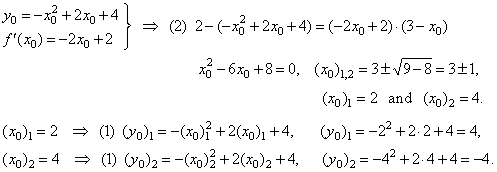
| Therefore, the points of tangency
are (2,
4)
and (4, -4). |
| To
write the equations of tangents t1
and t2
we calculate |
| their
slopes m1
and m2
from |
| f
'
(x0)
= -
2x0
+ 2. |
| Thus,
m1
=
f
'
(2)
= -
2
· 2
+ 2
= -
2,
m1
= -
2, |
|
and m2
=
f
'
(4)
= -
2
· 4
+ 2
= -
6,
m2
= -
6. |
| The
tangent
t1
through the point (2,
4)
and m1
= -
2, and |
| the
tangent
t2
through the point (4, -4)
and m2
= -
6, |
| t1 ::
y
= -
2x
+ 8
and
t2 ::
y
= -
6x
+ 20. |
|
 |
|
|
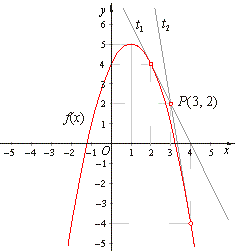Check
the coordinates of the points of tangency by plugging the
corresponding parameters into the above
formulas.
|
|
