|
|
|
Derivatives
of basic or elementary functions |
| Determining
the derivative of a function as the limit of the difference
quotient |
|
The
derivative of the exponential function |
|
The
derivative of the logarithmic function |
|
Differentiation
rules |
|
The
derivative of the sum or difference of two functions |
|
The
product rule |
|
A
constant times a function rule |
|
Derivatives of functions, examples |
|
|
|
|
|
|
| The
derivative of the exponential function |
|
Let
use the limit of the
difference quotient to find the
derivative of the function f
(x)
= ax. |
|
Since
the
difference quotient is
|
 |
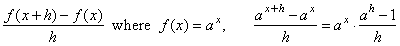| then,
the derivative as the limit of the difference quotient as h
tends to zero |
 |
|
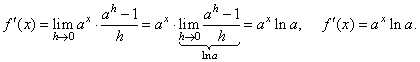That
is, by plugging t
= ah -
1, then t
®
0
as h ®
0,
and
|
 |
 |
| |
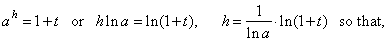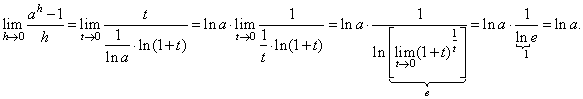Therefore,
if
|
f(x)
= ax |
then |
 |
|
|
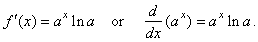| or
when the base a
is substituted by the natural base e
obtained is the exponential function ex,
thus
|
| |
if
|
f(x)
= ex |
then |
 |
|
|
|
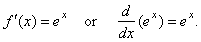| The
derivative of the logarithmic function |
| Let's
use the limit of the
difference quotient to find the
derivative of the function f
(x)
= loga x. |
| The
difference quotient applied to the given function |
 |
|
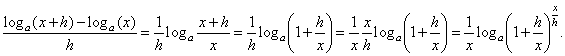As
the derivative is the limit of the difference quotient as h
tends to zero, then
|
 |
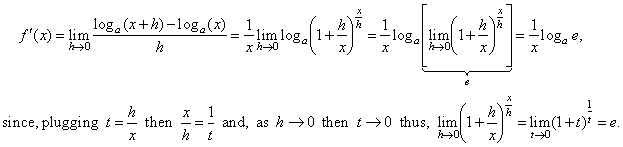| Then, applying the base
change identity and substituting a
= e |
 |
| |
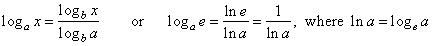if
f(x)
= loga x |
then |
 |
|
|
| |
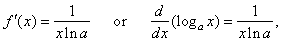if
f(x)
= ln x |
then |
 |
|
|
|
|
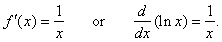| Differentiation
rules |
| The
derivative of the sum or difference of two functions |
| The
derivative of the sum or difference of two differentiable functions
equals the sum
or difference of their derivatives,
written |
|
|
|
| The
product rule |
| The
derivative of the product of two differentiable functions is
equal to, the first function times the derivative of the second
plus the second function times the derivative of the first, |
|
|
|
| A
constant times a function rule |
| The
derivative of a constant times a function is equal the constant
times the derivative of the function, where
the
constant c
can be any real number or expression that does not contain the
variable, |
|
|
|
|
| Derivatives of
functions examples |
| Example: |
Find
the derivative of the linear function f(x)
= m x
+ c. |
|
| Solution: |
 |
|
|
|
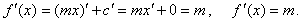| Example: |
Find
the derivative of the function |
 |
|
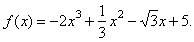| Solution: |
 |
|
|
|
|
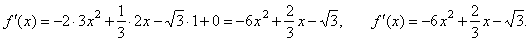| Example: |
Find
the derivative of the function |
 |
|
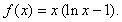| Solution: |
 |
|
|
|
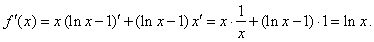| Example: |
Find
the derivative of the function |
 |
|
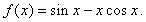| Solution: |
 |
|
|
|
|
|
|
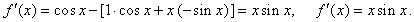