|
| Integral
calculus |
|
|
Applications
of the definite integral
|
 Length
of plane curve arc length
Length
of plane curve arc length
|
|
Arc length
of a parametric curve
|
|
Arc length of a curve in polar coordinates
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Length
of plane curve, arc length
|
|
The
length of an element dl
of a curve approximates to
|
|
|
|
The limit of the sum of such elements, as their number increases
to infinity and each increment dx
tends to zero, represents the
length L
of the curve.
|
|
|
|
Thus,
if f
is continuously differentiable on the closed interval [a,
b], the length of the
curve y = f
(x) from
x = a
to x = b
is
|
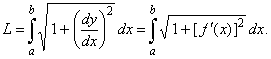
|
|
|
|
Example:
Find the arc length of
the upper semicircle of the circle x2
+ y2 = r2.
|
| Solution: Let
first calculate the derivative of the upper semicircle |
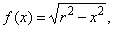 |
|
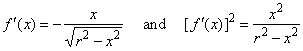 |
| then, using the above
formula for the arc length |
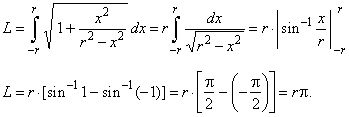 |
|
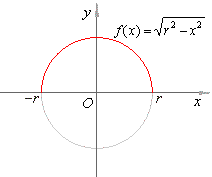 |
|
|
Therefore,
the circumference of a circle is 2rp.
|
|
|
|
Arc length of a parametric curve
|
|
If
a curve is given by the parametric equations x
= f (t) and
y = g (t)
such
that the derivatives, f
' and g'
are continuous
on the closed interval [t1,
t2]
from f (t1)
= a to f
(t2) = b,
so that
|
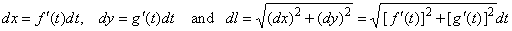
|
|
then,
|
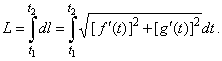
|
|
|
|
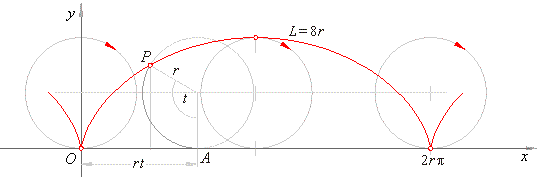
Example:
Find the arc length of
the common cycloid x =
r (t -
sin t)
and y
= r (1 -
cos t)
inside the
interval 0
<
t <
2p,
as is shown in the below figure.
|
|
Solution: The common cycloid is the
curve described by a fixed point on the circumference of a circle with the radius
r,
as the circle rolls without slipping on a straight line.
|
|
|
The circle rolls without slipping,
then arc PA
= OA = r
t therefore
|
|
P (x,
y)
where,
x =
r t -
r cos (t
-
p/2)
= r (t -
sin t)
and y
= r + r sin (t -
p/2)
= r (1 -
cos t).
|
|
Since,
|
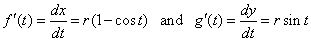
|
|
then, using the above
formula for the arc length of a parametric curve
|
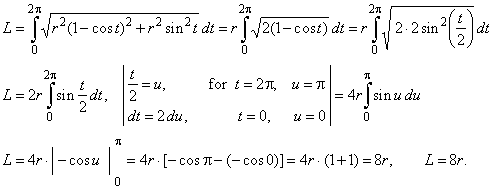
|
|
|
|
Arc length of a curve in polar coordinates
|
|
Suppose given a curve in polar
coordinates by r
= r (q
)
where q
changes inside the interval a
<
q
<
b
while a point passes along the arc from a
to
b.
|
|
To find the arc length of a curve in
polar coordinates we use the equations that relate Cartesian and
polar coordinates
|
|
x = r cos q
and y
= r sin q,
where
r
denotes r(q
)
|
|
and calculate differentials dx
and dy
applying the chain rule
|
|
dx
= cosq
dr -
r sinq
dq
and dy
= sinq
dr + r cosq
dq
|
|
so that,
|
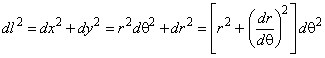
|
|
therefore,
|
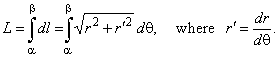
|
|
|
|
Example:
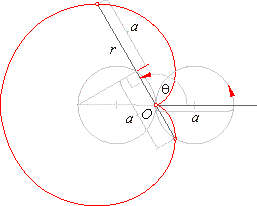
Find the length of
the cardioid r
= a (1 -
cosq
) shown in the below figure.
|
|
Solution: The cardioid is a
heart-shaped curve generated by a fixed point on a circle as it
rolls round another
circle of the same radius. The
diameter of circles is
a,
and q
is the polar angle.
|
| Since
r
= a(1 -
cosq
) then r'
= a sinq |
| so
that, r
2 + r'
2 = 4 a2 sin
2(q
/2).
|
| Using the above formula
for the length of a curve in |
|
polar coordinates |
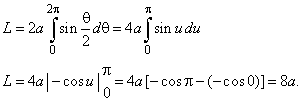 |
|
 |
|
|
Therefore, the length of the cardioid
equals eight diameters of the circles.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| Functions
contents G |
|
|
 |
|
| Copyright
© 2004 - 2020, Nabla Ltd. All rights reserved. |