|
| Integral
calculus |
|
|
Applications
of the definite integral
|
 The
volume
of a solid of revolution
The
volume
of a solid of revolution
|
|
The
volume
of a sphere
|
|
The
volume
of a spherical segment
|
|
The
volume
of a cone
|
|
|
|
|
|
|
|
|
|
|
|
|
|
The
volume
of a solid of revolution
|
|
A solid figure generated by revolving
a given curve around an axis of revolution is called the solid of
revolution.
|
|
The volume generated by the region of
the coordinate plane bounded by the segment of a curve y
= f (x)
between x
= a, y
= b and the x-axis, revolving around
the x-axis,
is shown in the left figure below.
|
|
Note that the infinitesimal volume of
the cylinder representing an element of the integration,
|
|
dV = area
´
width = py2
´
dx.
|
|
|
|
The volume generated by the segment of
a curve x = g
(y) between y
= c and y
= d, revolving around
the
y-axis,
is shown in the right figure above.
|
|
|
|
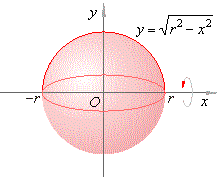
The
volume
of a sphere
|
| Example:
Find the volume of a
sphere generated by a semicircle |
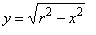 |
revolving around
the |
|
|
x-axis.
|
|
Solution: Since the endpoints of the
diameter, lying |
| on the
x-axis,
are -
r and r,
then
|
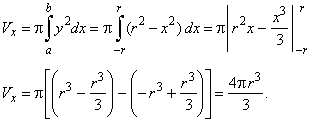 |
|
 |
|
|
|
|
The
volume
of a spherical segment
|
|
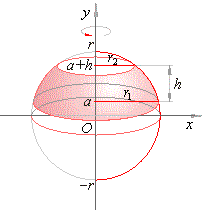
Example:
Find the volume of a
spherical segment generated by the portion of the right semicircle
between y = a
and y = a
+ h, revolving around
the y-axis,
as
is shown in the below figure.
|
|
Solution: Since the right semicircle
equation |
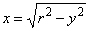 |
then
|
|
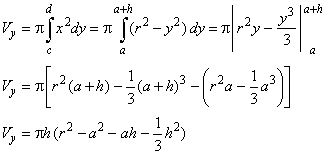 |
| or,
by substituting r12
= r2 -
a2 and
r22 =
r2 -
(a + h)2 |
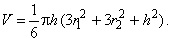 |
|
 |
|
|
|
|
The
volume
of a cone
|
|
Example: Find the volume of a
right circular cone generated by the line (segment) passing through
the origin and the point (h,
r), where h
denotes the height of the cone and r
is the radius of its base, revolving around the x-axis,
as shows the below figure.
|
|
Solution: The equation of the
generating line
|
|
|
|
|
|
Example:
Find the volume of
a solid of revolution generated by a plane bounded by the segment of a curve
y
=
- x2
+ 3x and the x-axis,
revolving around
the x-axis,
as shows the below figure.
|
|
Solution: The limits of the integration
- x2
+ 3x
= 0,
|
|
x(-x
+ 3)
= 0, x1
= 0 and x2
= 3
then,
|
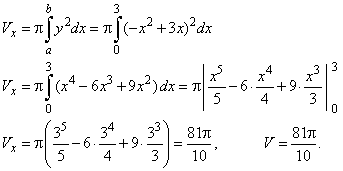 |
|
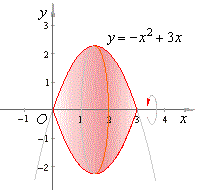 |
|
|
|
|
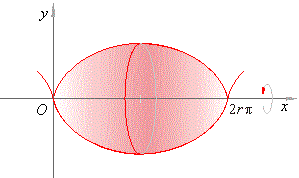
Example:
Find the volume of
a solid of revolution generated by one cycle of the cycloid x =
r (t -
sin t),
y
= r (1 -
cos t)
and the x-axis,
revolving around
the x-axis,
as shows the below figure.
|
|
|
Solution: Since y2
= r2(1 -
cos t)2,
dx = r (1
-
cos t)dt
the limits of the integration
0 <
t <
2p,
then
|
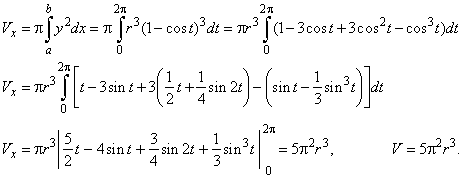
|
|
|
|
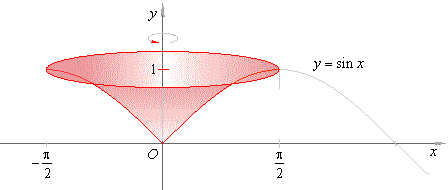
Example:
Find the volume of
a solid of revolution generated by the arc of the sinusoid y
= sin x between
x = 0 and x
= p/2,
revolving around
the y-axis,
as shows the below figure.
|
|
|
|
|
Solution: Since curve
rotates around
the y-axis,
we should apply the inverse of the sine, i.e., we use
x
= g (y) form or x
= arcsin y = sin-1y.
Thus, the limits of the integration,
for x1
= 0, y1
= 0 and for x2
= p/2, y2
= 1 then, applying
the integration by parts twice
|
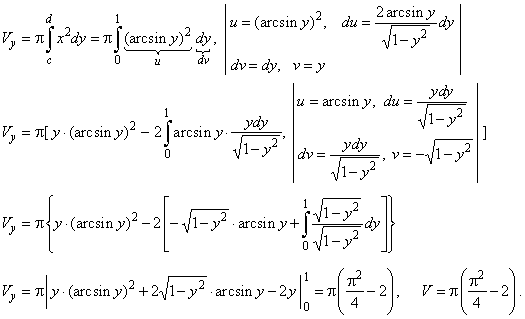
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| Functions
contents G |
|
|
 |
|
| Copyright
© 2004 - 2020, Nabla Ltd. All rights reserved. |