|
| Integral
calculus |
|
|
Applications
of the definite integral
|
 The
area between two curves
The
area between two curves
|
|
The
area between two curves examples
|
|
|
|
|
|
|
|
|
|
|
|
|
|
The
area between two curves
|
|
If
given are two continuous functions, f
and g
defined over an interval [a,
b],
with g
(x)
<
f (x)
for all x
in
[a,
b],
then the area A
of the region bounded (or enclosed) by these two curves and the
lines x
= a
and
x
= b
is
given by
|
|
|
|
|
|
The
area between two curves examples
|
|
Example:
Find the area of the
region bounded by the curve f
(x) = -
x2 - 2x
and the line g(x)
=
x.
|
|
Solution: To
find points of intersections (limits of integration) of the given
functions we solve their equations,
|
| -
x2 - 2x =
x
or
x2 + 3x = 0, |
| x(x
+ 3) = 0,
x1 = 0 and
x2
= -3. |
| Thus,
the area |
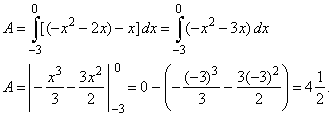 |
|
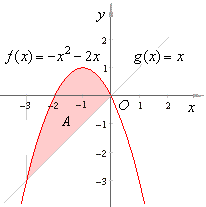 |
|
|
|
|
Example:
Find the area of the
region lying to the left of the y-axis
and enclosed by the curves,
|
|
f
(x) = (1/3)x3 -
3x and g(x) =
x2 + 3x.
|
|
Solution: To
find points of intersections (limits of integration) of the given curves
we solve their equations,
|
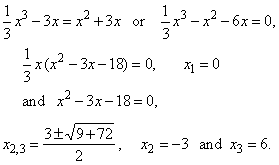 |
| Thus,
the area |
|
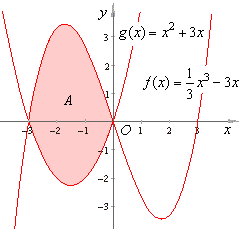 |
|
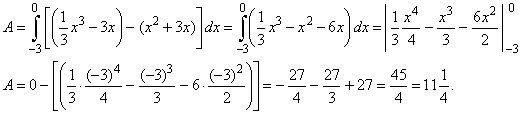
|
|
|
|
Example:
Find the area of the
region bounded by the curve y2
=
x and the line y
= -
x
+ 2.
|
|
Solution: To
find points of intersections (limits of integration) of the given curve
and the line we solve their
|
| equations,
(-
x
+ 2)2 =
x
or x2
-
5x + 4 = 0, |
| (x
-
1)(x
-
4) = 0,
x1 = 1 and
x2
= 4. |
| Thus,
the area |
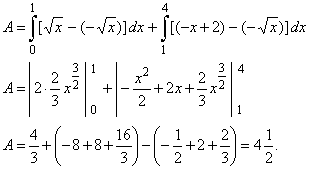 |
|
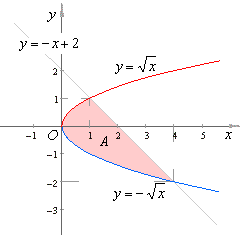 |
|
|
The same area can be calculated by
changing the role of the variables (or the coordinate axes) to get simpler integral expression, therefore
|
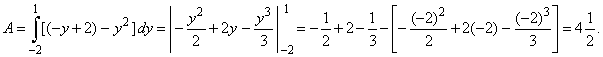
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| Functions
contents G |
|
|
 |
|
| Copyright
© 2004 - 2020, Nabla Ltd. All rights reserved. |