|
| Integral
calculus |
|
|
Applications
of the definite integral
|
 The
area of a region in the plane
The
area of a region in the plane
|
|
The
area between the graph of a curve and the coordinate axis
|
|
The
area between the graph of a curve and the coordinate axis examples
|
|
The
area bounded by a parametric curve
|
|
The
area of the sector of a curve in polar coordinates
|
|
The
area of the sector of a curve given in Cartesian (or rectangular) coordinates
|
|
The
area of the sector of a parametric curve
|
|
|
|
|
|
|
|
|
|
|
|
|
|
The
area of a region in the plane
|
|
The
area between the graph of f (x) and the x-axis
|
|
If
given a continuous nonnegative function f
defined over an interval [a,
b] then, the area A
enclosed by the
curve y
= f (x),
the vertical lines, x
= a and x
= b and the x-axis,
is defined as
|
|
|
|
|
|
The
area between the graph of a curve and the coordinate axis examples
|
|
Example:
Find the area between
the graph of f
(x) = -
(1/3)x3 + 3x
and the x-axis
over the interval defined by two nonnegative successive
roots of the given cubic.
|
|
Solution: To
find roots we should solve f
(x) = 0,
|
|
|
|
|
|
Example:
Find the area between
the curve x = -
y2 + y
+ 2 and the y-axis.
|
|
Solution: Since
given curve is the parabola whose axis of symmetry is
parallel to the x-axis
we first calculate its
y-intercepts
by setting x =
0 to determine the limits of
integration,
|
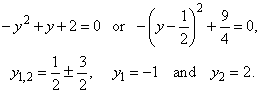 |
|
| Thus,
the area |
|
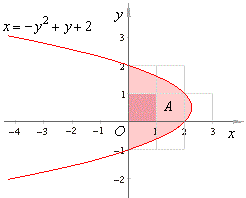 |
|
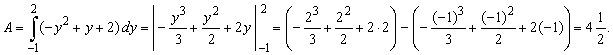
|
|
|
|
Example:
Find the area of the
ellipse b2x2 +
a2y2 = a2b2
that is symmetrical about
the coordinate axes
and that intersects the coordinate axes at the
points (+ a,
0) and (0,
+
b).
|
|
Solution: Let
write the ellipse in the explicit form y
= f (x)
|
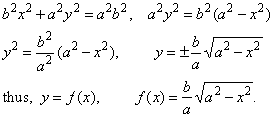 |
| Thus,
we calculate the area A
using the solution of |
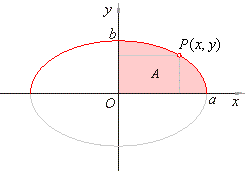
| the
indefinite integral example 48. that is |
|
 |
|
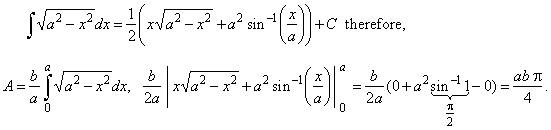
|
|
Hence, the area of the ellipse is abp,
and by setting b
= a we get the area of
the circle
a2p.
|
|
|
|
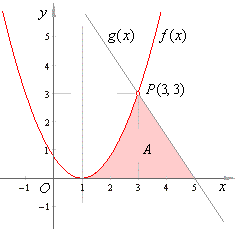
Example:
Find the area A
enclosed
by the parabola, the line and the x-axis
shown in the below figure.
|
|
Solution: First we should find
the equation of the parabola and the line using given points.
|
|
The parabola is translated in the
direction of the x-axis
by x0
= 1, so
that
|
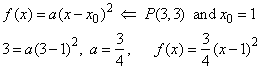 |
| and the line |
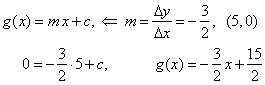 |
| Thus,
the area |
|
 |
|
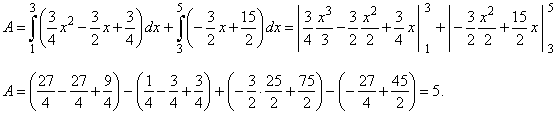
|
|
|
|
The
area bounded by a parametric curve
|
|
If
a curve is given by the parametric equations x
= f (t) and
y = g (t), then
the area enclosed by the curve,
the vertical lines, x
= a and x
= b and the x-axis,
we
obtain from
|
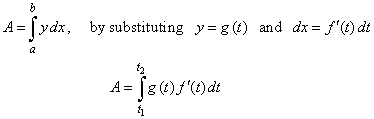
|
|
where,
f (t1) = a
and f (t2)
=
b,
g (t)
>
0
inside
[t1,
t2].
|
|
|
|
Example:
Find the area bounded
by the
ellipse x = a
cos t,
y = b
sin t,
( 0 <
t <
2p
).
|
|
Solution:
As the ellipse is symmetrical about
the coordinate axes we will calculate quarter of the area.
|
|
By substituting x
= 0 and x
= a into the
equation x = a
cos t and
solving for
t,
we get the limits of integration
t1 =
p/2
and t2 =
0
respectively.
|
|
Therefore,
|
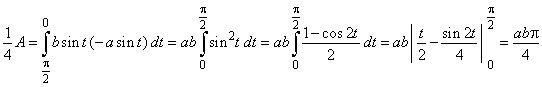
|
|
so that, the area of the ellipse
A = abp.
|
|
|
|
The
area in polar coordinates
|
|
Polar coordinates (
r, q )
locate a point in a plane by means of the length r,
of the line joining the point to the origin or pole
O,
and angle q
swept out by that line from the polar axis.
|
|
Recall the area A
of a circular sector bounded by two radii and an arc, is defined
by the proportion
|
|
A : r2
p
= q
: 2p
thus, A
= (1/2) r2q
|
|
where r
is the length of the radius and q
is the central angle subtended by the arc.
|
|
Suppose given a curve in polar
coordinates by r
= f (q
)
or
r
= r
(q
)
then, the area of the region bounded by the curve and the radii that correspond to
q
1 = a
and q
2 = b,
is given by
|
|
|
|
|
|
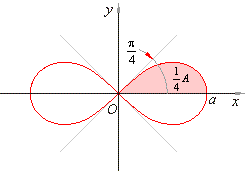
Example:
Find the area of the
region enclosed by the lemniscate of Bernoulli whose polar equation
is
r2 = a2
cos2q,
shown in the below figure.
|
|
Solution: As the
lemniscate consists of two symmetrical loops meeting at a node, we will calculate quarter
of the
area lying inside 0
<
q
<
p/4.
|
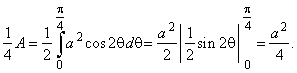 |
| Thus,
the area of the lemniscate A
= a2. |
|
 |
|
|
|
|
The
area of the sector of a curve given in Cartesian or rectangular coordinates
|
|
We
use the formulas for conversion between Cartesian and polar
coordinates,
|
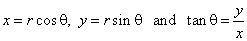
|
|
to find the area of the sector bounded by
two radii and the
arc P0P,
of a curve y
= f (x) given in the
|
|
Cartesian coordinates, where x
is the value inside the interval [a,
b]. Then
|
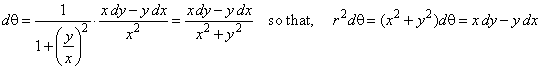
|
|
therefore,
|
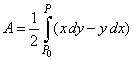
|
|
is the area of the sector bounded by
two radii and the arc P0P
of a curve y
= f (x).
|
|
|
|
The
area of the sector of a parametric curve
|
|
The area of the sector bounded by two
radii and the arc P0P
of a parametric curve is given by
|
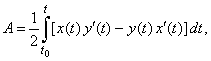
|
|
where the parametric values, t0
and t
relate to the endpoints, P0
and P
of the arc, respectively.
|
|
|
|
Example:
Find the area of the
sector of the rectangular hyperbola x2
-
y2 = 1
enclosed by the
x-axis, the arc of the right branch of the
hyperbola between the vertex and the point
P(cosh
t,
sinh
t), and the
line joining this point to the origin, as shown in
the below figure.
|
|
Solution: Since the hyperbolic functions satisfy the identity
cosh2
t
-
sinh2 t
= 1 then, the point
x = cosh
t and
y = sinh
t
that lies on the
hyperbola x2
-
y2 = 1,
describes the right branch of the
hyperbola as parameter
t increases from
-
oo
to +
oo.
|
|
The point traces the hyperbola passing from negative infinity, through
P0
(t = 0) to positive
infinity.
|
| As,
x'
(t) = sinh
t
and
y' (t) = cosh
t, |
| so
that x(t)
y' (t) = cosh2
t
and
y(t) x' (t) = sinh2 t, |
| and
by using the above formula for the area of the
sector |
| of
a parametric curve |
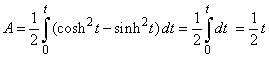 |
| we
get the area of the sector P0OP
of the rectangular hyperbola. |
|
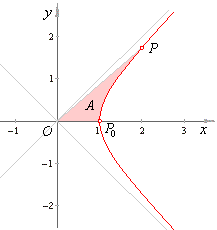 |
|
|
Therefore, the parameter (or argument)
t,
of hyperbolic functions, is twice the area of the sector P0OP,
i.e., t = 2A.
That is why the inverse hyperbolic functions are also called the
area functions.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| Functions
contents G |
|
|
 |
|
| Copyright
© 2004 - 2020, Nabla Ltd. All rights reserved. |