|
| Integral
calculus |
|
 Differentiation
and integration of infinite series
Differentiation
and integration of infinite series
|
|
Differentiation
of power series |
|
Differentiation
and integration of infinite series example
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Differentiation
and integration of infinite series
|
|
If
f (x)
is represented by the sum of a power series
|
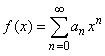
|
|
with
radius of convergence r
> 0 and -
r < x < r,
then the function has the derivative
|
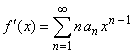
|
|
and
the function has the integral
|
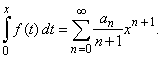
|
|
Thus,
a power series can be differentiated
and integrated term by term while the radius of convergence
remains
the same, with only (possible) exception at the endpoints of the
interval of convergence.
|
|
|
| Differentiation
of power series |
|
Recall
that the exponential function f
(x)
= ex
represented
by the power
series
|
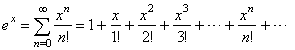 |
| is absolutely convergent for all real x
since |
| by
the ratio test |
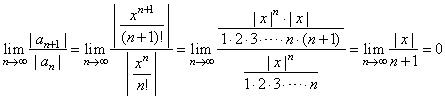 |
|
| the
limit L
< 1 for
any value of x. |
|
Applying the power rule
|
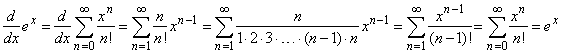 |
|
thus, for all real x
the function f (x)
= ex is equal
to its own derivative f
' (x).
|
|
|
| Example:
Find |
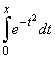 |
by
representing
the integrand function as the power series. |
|
| Solution: By
substituting -
x2
for x
in the above power series expansion of ex
we get |
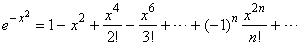 |
| Let
write down the initial sequence of nth
order polynomials that describe the function for all real x, |
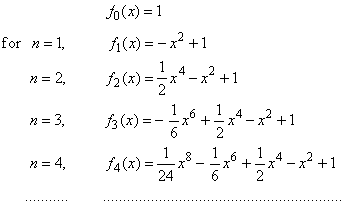 |
| Since
every polynomial above is missing the preceding odd degree term, their
coefficient an-1
= 0 |
| thus, the coordinates
of translations |
|
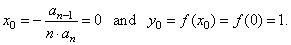 |
|
|
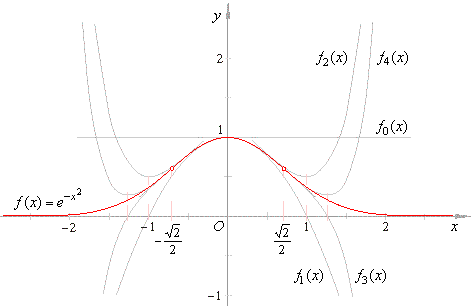
| Therefore,
the polynomials that describe the function
all are
source polynomials of even degree translated in |
| the
direction
of the y
axis by y0
= 1, as is shown in the picture below.
|
|
|
Note that the roots of odd indexed
polynomials in the series correspond to the abscissas of
successive even indexed polynomials, as shows the above graph.
|
|
On the graph of the bell-shaped curve,
representing the probability density function of a normal
distribution, at
x = ±
Ö2/2
denoted are the points of
inflections.
|
|
Therefore, the power series representing the
normal curve converges for all real x.
|
|
Hence, by integrating the series term
by term obtained is
|
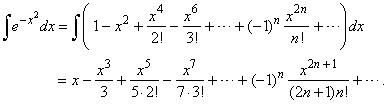 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| Functions
contents G |
|
|
 |
|
| Copyright
© 2004 - 2020, Nabla Ltd. All rights reserved. |