|
| Integral
calculus |
|
|
The
definite and indefinite integrals |
 The indefinite integral
The indefinite integral |
|
Integration - inverse of differentiation |
|
Constant
of integration, the arbitrary constant term in the expression of the
indefinite integral |
|
Evaluating the indefinite integral example |
|
|
|
|
|
|
|
| The
indefinite
integral |
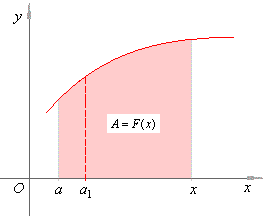
| Assume
the lower limit a
of an integral is fixed and the upper limit is changing. Then, starting
from the fixed
ordinate at a,
also changes the area A
under the curve as its endpoint ordinate moves parallel. |
| As
we evaluate the integral over an interval whose right-hand endpoint x
changes, the actual value of the area is
a function of x
usually denoted F(x),
so that |
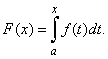 |
|
The integral F (x)
is called the indefinite integral of f
(x). Note
that the variable of integration is replaced by the letter t
as x now denotes the upper limit. |
|
 |
|
|
Note also that, the value of the above integral will change whether lower or
upper limit of integration changes. |
|
So for example, we choose other fixed point a1
instead of a,
such that
a1
> a then |
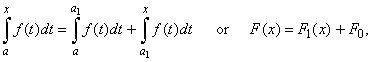 |
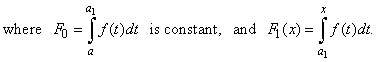 |
|
Thus, as the point a1
can be placed anywhere inside the interval [a,
x], the same
function f (x)
has infinite number
of indefinite integrals that differ only in a constant value F0
that correspond to any chosen area
over the
interval [a,
a1],
as shows the above figure. |
|
| Integration
inverse of differentiation |
|
We should use the process inverse of differentiation to find function F
(x)
whose derivative is given function f. |
| Therefore,
if F (x)
is defined to be the integral of f
(x)
from a
to x
for all x
in [a,
b], written |
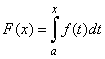 |
| then,
f
is derivative of F
at every point of the interval at which f
is continuous. |
| This
means that for any x
in (a,
b),
F' (x)
= f
(x). |
| Every
such function F(x)
is called an antiderivative or primitive
of a given function f (x).
As, |
|
dF = F' (x)
dx
= f (x) dx |
| the
same process we also can read, how to find the antiderivative F(x)
whose differential f
(x)dx
is given. |
|
Thus for example, if given |
| f
(x)
= 1 then F
(x)
= x, or if f
(x)
= 2x then F(x)
= x2, or if f
(x)
= sin x then F
(x)
= -
cos x and so on. |
| But
as well, antiderivatives of these f
(x)
respectively are, |
| F
(x)
= x + C,
F (x)
= x2 + C,
F (x) = -
cos x + C, and so
on |
| regardless
of the value of the constant C. |
| Recall
that, according to the mean value theorem, functions that have the same
derivatives at every point of an
interval differ in a constant term only. |
| Therefore,
if F (x)
is one of the antiderivative functions of a given f
(x)
then, others are of the form F
(x)
+ C, where C
is any constant. Graphically, they represent the same function
translated in the direction of the y-axis
by the constant C. |
|
| Constant
of integration, the arbitrary constant term in the expression of the
indefinite integral |
| Recall
that, the constant F0, as part of the expression
F (x) = F1(x) +
F0, that
comes from the change of the lower limit of integration, as the value in
which differ the indefinite integrals of the same function, does not
include all antiderivatives. |
| Thus, for example the expression
F (x) =
x2 + C includes
all antiderivatives or primitive
functions of |
| f
(x) =
2x since C
can be any positive or negative constant, while the same indefinite
integral when |
| evaluated
using the definition |
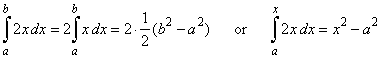 |
|
| yields
the negative constant -
a2. |
| To
ensure that the indefinite integral coincides with the meaning of
antiderivative or primitive function it is necessary
add an arbitrary constant term to its definition, regardless of the lower
limit a,
so that |
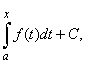 |
where C
is an arbitrary constant, or written shorter |
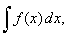 |
thus |
|
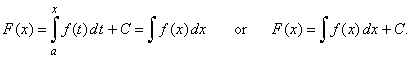 |
|
| Evaluating
the indefinite integral example |
| Example:
Given
f (x) = -
x2 + 4, find
its antiderivatives or primitive functions
F (x)
and draw their graphs. |
| Solution: Since
an indefinite integral is any function F
(x)
whose derivative is given f
(x),
then |
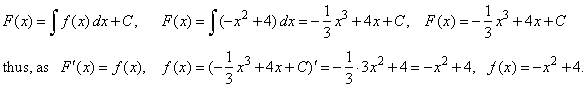 |
| Therefore,
obtained primitive functions F
(x)
are
represented by all source cubic functions y
= a3x3 + a1x
whose
graphs are translated in the direction of the y-axis
by y0
= C. |
| Let
for example C = -
3 then, the translated cubic y = (-1/3)x3
+ 4x -
3 represents one particular antiderivative
F (x),
as is shown in the figure below (colored blue). |
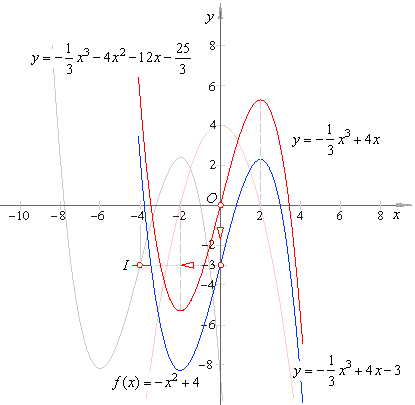 |
| If,
the graph of F (x)
we now translate, or move horizontally in the direction of x-axis
by x0 = -
4, that is, |
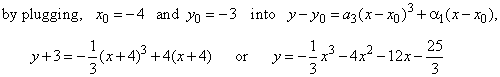 |
| we
get the cubic explored in the section ' Applications
of differentiation - the graph of a function and its derivative'. |
|
|
|
|
|
|
|