|
| Integral
calculus |
|
|
The
definite and indefinite integrals |
 The indefinite integral
The indefinite integral |
|
Evaluating the indefinite integral example |
 The fundamental theorem of
calculus
The fundamental theorem of
calculus |
|
The fundamental theorem of differential calculus |
|
|
|
|
|
|
|
| Evaluating
the indefinite integral example |
| Example:
Given
f (x) = -
x2 + 4, find
its antiderivatives or primitive functions
F (x)
and draw their graphs. |
| Solution: Since
an indefinite integral is any function F
(x)
whose derivative is given f
(x),
then |
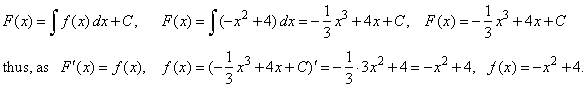 |
| Therefore,
obtained primitive functions F
(x)
are
represented by all source cubic functions y
= a3x3 + a1x
whose
graphs are translated in the direction of the y-axis
by y0
= C. |
| Let
for example C = -
3 then, the translated cubic y = (-1/3)x3
+ 4x -
3 represents one particular antiderivative
F (x),
as is shown in the figure below (colored blue). |
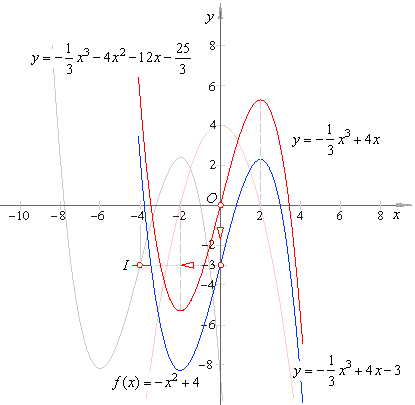 |
| If,
the graph of F (x)
we now translate, or move horizontally in the direction of x-axis
by x0 = -
4, that is, |
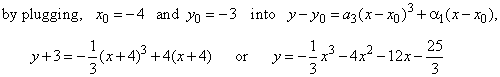 |
| we
get the cubic explored in the section ' Applications
of differentiation - the graph of a function and its derivative'. |
|
| Let's
prove that the differentiation of an indefinite integral with respect to
the variable upper limit yields the function
that
is integrated, the integrand. |
| Let
write the increment DF
of the difference quotient DF/Dx |
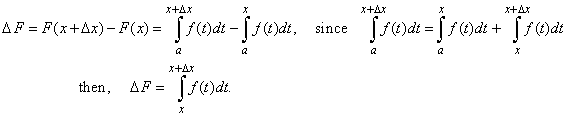 |
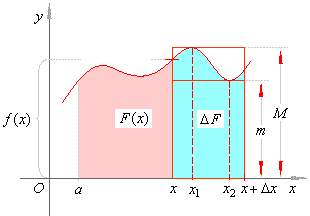
| As f(x)
is continuous function in the closed interval |
| [x,
Dx]
it takes its maximal value M
and minimal |
| value m
at some points, x1
and x2,
as is shown in |
| the right
figure. |
| Therefore,
according to the mean value theorem |
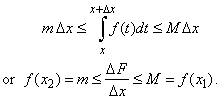 |
|
 |
|
| Now,
as Dx
®
0
then x
+ Dx
tends to x,
and since f
is continuous then f
(x1)
and f (x2)
approach f (x). |
| Thus, |
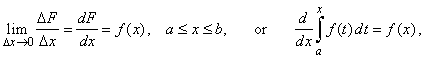 |
|
|
that is, by differentiating the indefinite integral of a
continuous function with respect to
the upper limit x
we get the
function that
is integrated (the integrand). Hence, we also can write |
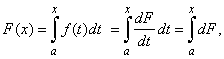 |
| that
is, by integrating the derivative F' (x),
or the differential dF,
we get the antiderivative F
(x). |
| Therefore,
differentiation and integration are inverse-related operations, when
successively performed on the same
continuous function, the function stays unchanged. So, by integrating a
continuous function f
we get a new
function which, when differentiated, leads back to the original function
f. |
| This property we use to check the result of integration thus, by differentiating the result of integration we must obtain the integrand
(the function that is integrated). |
| Similarly,
differentiation of the indefinite integral with respect to
the lower limit we write as |
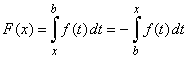 |
| so
that, F' (x)dx
= -
f (x). |
| Therefore,
the indefinite integral of a continuous function f
(x)
is any of its antiderivatives or primitive functions (whose derivative is
f (x)). |
|
|
The fundamental theorem of calculus |
| The
theorem that states the relationship between integration and
differentiation, that is, between areas and tangent
lines, is called the fundamental theorem
of calculus |
|
|
The fundamental theorem of differential calculus |
| If
f (x) is continuous on
closed interval [a,
b] and F
(x)
is defined to be |
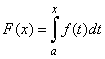 |
| then,
F
is differentiable on (a,
b)
such that F' (x)
= f (x) for all x
in (a,
b).
This means that |
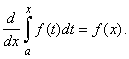 |
|
| Evaluating definite integrals
using indefinite integrals |
| To
evaluate the definite integral |
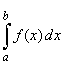 |
we should find one
primitive function F
(x)
or antiderivative of |
|
|
the function f (x),
and since the indefinite integral |
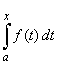 |
is a primitive
function of f
(x)
then, as two |
|
| primitives
of the same function can differ only by a constant, we can write |
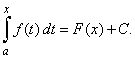 |
| To
find the value of the constant C
that belongs to the lower limit a,
substitute x = a
to both sides of the |
| above equality, and
since |
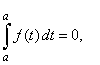 |
then C
= -
F(a),
so that |
|
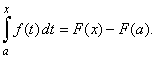 |
| Therefore,
the
definite and indefinite integrals are related by the fundamental theorem
of calculus. |
| This
result shows that integration is inverse of differentiation. |
|
| The fundamental theorem of integral calculus |
| If
f (x)
is integrable on the interval [a,
b]
and F (x)
is an antiderivative of f
on (a,
b),
then |
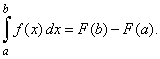 |
| The
right side of the above equation we usually write |
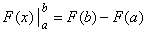 |
| so
that, |
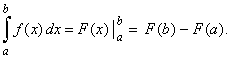 |
|
|
| Thus,
to evaluate the definite integral we need to find an atiderivative F
of f,
then evaluate F (x)
at x = b
and at x
= a, and calculate the
difference F (b)
-
F (a). |
|
|
|
|
|
|
|