|
| Integral
calculus |
|
|
The
definite and indefinite integrals |
 Properties of the definite integral
Properties of the definite integral |
|
The definite integral
over interval of zero length |
|
Reverse
order of integration |
|
The constant multiple rule |
|
The integral of the sum or difference of two functions |
|
Internal addition of the definite integral |
|
The definite integral of an odd function |
|
The definite integral of an even function |
|
The definite integral of a nonnegative and nonpositive functions |
|
Relationship of the definite integrals of two functions over the same
interval of integration |
|
Absolute integrability |
|
The mean value theorem |
|
The average value of a function over the given interval |
|
|
|
|
|
|
|
| Properties
of the definite integral |
| 1)
The definite integral
over interval of zero length |
| Since
the definite integral we evaluate as the limit of Riemann sums, the
basic properties of limits hold for integrals
as well. |
| Thus, the limit of Riemann sums show
the first property
|
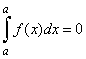 |
| as
the upper limit b
tends to lower limit a,
written b
®
a. |
|
| 2)
Reverse
order of integration |
| By
reversing the upper and lower limits of integration to b
< a, that is, passing
through the x-axis
from a
to b in
opposite direction, each difference, x1
-
a, x2 -
x1, . . . , b -
xn
- 1
of Riemann sums becomes negative
while function values, f
(xi')
can stay unchanged, therefore |
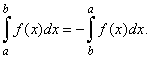 |
| The definite integral
changes sign if the limits of integration interchange. |
|
| 3)
The constant multiple rule |
| Suppose
f
(x) is integrable over the
interval [a,
b] and c
is any real number, then c
f
(x) is integrable over
[a,
b] such that |
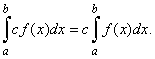 |
| If
integrand is multiplied by a constant, we can factor out the constant. |
|
| 4)
The integral of the sum or difference of two functions |
| Suppose
f(x)
and g(x)
are integrable over the
interval [a,
b] then |
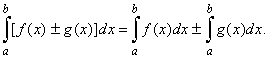 |
| The
integral of the sum or difference of two functions is the sum or
difference of the integrals of each function |
|
| 5)
Internal addition of the definite integral |
| Suppose
f
(x)
is integrable over the
interval [a,
b] and c
is a point inside the interval, i.e., a
< c < b then, the
additive
property of the definite integral holds |
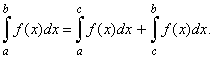 |
| Let
for example c
lies outside the interval such that c
< a < b, and
assume f
(x)
is integrable over the
interval [c,
b] then, |
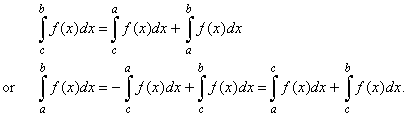 |
| Therefore,
the above rule holds for any arrangement of three points, a,
b
and c. |
|
| 6)
The definite integral of an odd function |
| If
the integrand is an odd function f
(x) = -
f
(-x),
the graph of which is symmetrical about the origin, with the
interval of integration [-
a,
a],
then |
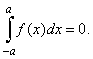 |
|
| 7)
The definite integral of an even function |
| If
the integrand is an even function f
(x) = -
f
(x), the graph of
which is symmetrical about the y-axis,
with the
interval of integration [-
a,
a],
then |
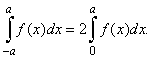 |
|
| 8)
The definite integral of a nonnegative and nonpositive functions |
| Suppose
f
(x)
is integrable over the
interval [a,
b] and f
(x) >
0 but not identically
equal to zero, then |
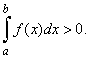 |
| If
f
(x)
is integrable over the
interval [a,
b] and f
(x) <
0 but not identically
equal to zero, then |
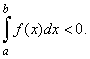 |
|
| 9)
Relationship of the definite integrals of two functions over the same
interval of integration |
| Suppose
f
(x) and g
(x) are integrable over the
interval [a,
b] and f
(x) >
g
(x) for all x
in [a,
b], then |
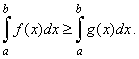 |
|
| 10)
Absolute integrability |
| Suppose
f
is integrable over the
interval [a,
b], it can be shown
that | f
(x)| is also
integrable on [a,
b] |
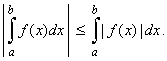 |
| Since,
-
|
f
(x)| <
f
(x) <
|
f
(x)|, then |
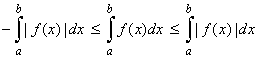 |
| what
means the same as the above. |
|
| 11)
The mean value theorem |
| Suppose f
(x)
is integrable over the
interval [a,
b] and m
and M
are minimal and maximal value of the function,
that is m
<
f
(x) <
M
for all x
in [a,
b], then |
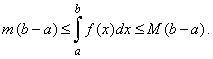 |
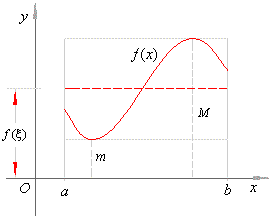
| Geometric
meaning of the above inequality is that the area under the graph of f
(x) over the
interval [a,
b] is contained inside
the rectangles with the same base (b
-
a)
and of the heights m
and M. |
|
Since f
(x)
is continuous in the
interval [a,
b] it |
| takes at least
one time each value between m
and M |
|
inside the interval. |
| Therefore, there is at least one
value x
inside the |
|
interval [a,
b] such that |
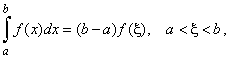 |
| meaning, there
exists the rectangle with the base |
|
 |
|
| (b
-
a)
and a height f
(x)
whose area equals the area under the graph of f
(x) over the
interval [a,
b]. |
|
| 12)
The average value of a function over the given interval |
| For
a continuous function f
over an
interval [a,
b], the average value
of f
(x) is defined as |
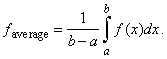 |
| Thus,
the average value of a function f
(x) over an
interval [a,
b] is equal to some
value of the function between
its minimal and maximal value inside the interval, as shows the above
figure. |
|
| The
indefinite
integral |
| Assume
the lower limit a
of an integral is fixed and the upper limit is changing. Then, starting
from the fixed
ordinate at a,
also changes the area A
under the curve as its endpoint ordinate moves parallel. |
| As
we evaluate the integral over an interval whose |
| right-hand endpoint x
changes, the actual value of the |
| area is
a function of x
usually denoted F(x),
so that |
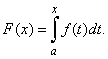 |
|
The integral F(x)
is called the indefinite integral of f(x). |
| Note
that the variable of integration is replaced by the |
| letter t
as x now denotes the upper limit. |
|
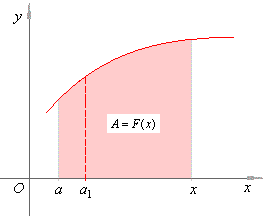 |
|
|
Note also that, the value of the above integral will change whether
lower or upper limit of integration changes. |
|
So for example, we choose other fixed point a1
instead of a,
such that
a1
> a then |
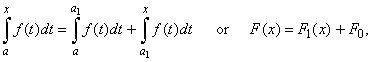 |
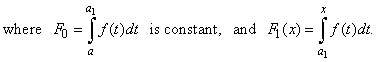 |
|
Thus, as the point a1
can be placed anywhere inside the interval [a,
x], the same function
f (x)
has infinite number
of indefinite integrals that differ only in a constant value F0
that correspond to any chosen area
over the
interval [a,
a1],
as shows the above figure. |
|
|
|
|
|
|