|
|
|
| Polynomial and/or Polynomial
Functions and Equations |
 Quadratic function
and equation
Quadratic function
and equation |
|
The
graph of quadratic function |
|
Translated form of
quadratic function |
|
The sum and product of
the roots |
|
Vertex (the turning
point, maximum or minimum) - coordinates of translations |
|
Transformations
of the graph of the quadratic function |
 Quadratic equation
word problems
Quadratic equation
word problems |
|
|
|
|
|
|
| Quadratic function
and equation |
| The
polynomial function of the second degree, f
(x)
=
a2x2
+ a1x
+ a0, is called a
quadratic function. |
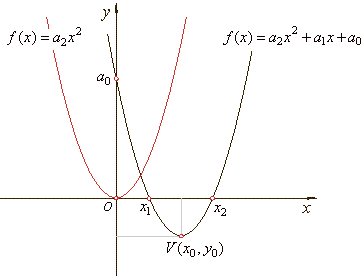 |
| |
y
= f (x)
=
a2x2
+ a1x
+ a0
or y
-
y0
= a2(x
-
x0)2, |
where |
|
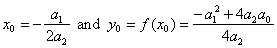 |
coordinates
of translations of the quadratic function. |
|
| By
setting x0
=
y0
= 0, we get |
y
=
a2x2,
the source quadratic function.
The turning point V
(x0,
y0). |
|
| The
real zeros of the
quadratic function: |
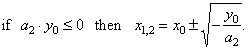 |
|
| |
y
= f (x) =
a2x2
+ a1x
+ a0 = a2(x
- x1)(x
- x2)
= a2[x2
-
(x1 +
x2)x
+
x1x2] |
|
| The graph of a quadratic function is curve called a parabola. The parabola is symmetric with respect to a vertical line
called the axis of symmetry. |
| As
the axis of symmetry passes through the vertex of the parabola
its equation is x
= x0. |
|
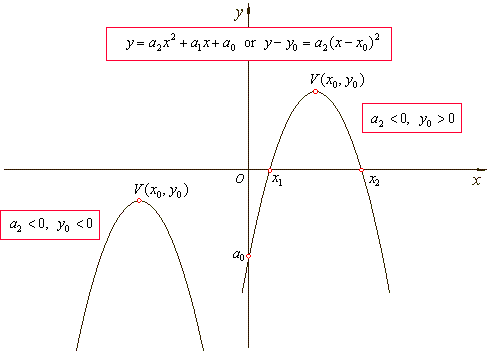
| Transformations
of the graph of the quadratic function |
| How
changes in the expression of the quadratic function affect its
graph is shown in the figures below. |
|
|
|
|
 |
|
The graph of quadratic polynomial will intersect the
x-axis in two
distinct points if its leading coefficient
a2 and the vertical translation
y0
have different signs, i.e., if a2
· y0
<
0. |
|
|
| Example:
Find zeros and vertex of
the quadratic function y
=
-
x2
+ 2x
+
3
and sketch its graph. |
| Solution:
A quadratic function can
be rewritten into translatable form y
-
y0
= a2(x
-
x0)2
by completing the square, |
|
y
=
-
x2
+ 2x
+ 3 |
Since a2
· y0
<
0 given
quadratic function must have two different real zeros. |
|
y
=
-
(x2
-
2x)
+ 3 |
To find zeros of a function, we set
y
equal to zero and solve for x.
Thus, |
|
y
=
-
[(x
-
1)2
-
1]
+ 3 |
-
4
=
-
(x
-
1)2 |
| y -
4
=
-
(x
-
1)2 |
(x
-
1)2
=
4 |
| y
-
y0
= a2(x
-
x0)2 |
x
-
1
=
+ sqrt(4) |
| V(x0,
y0)
=> V(1,
4) |
x1,2
=
1
+
2, => x1
= -
1
and x2
= 3. |
|
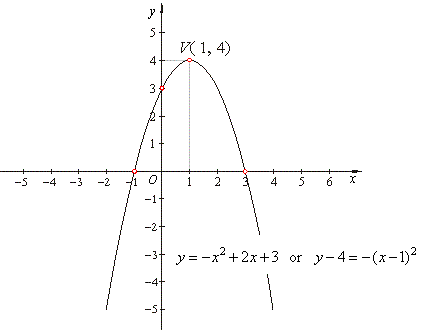 |
| We
can deal with given quadratic using the property of the
polynomial explored under the title, 'Transformations of the polynomial function
applied to the quadratic and cubic functions' above. |
| Thus, |
| 1)
calculate the coordinates of translations of the quadratic
y
=
f (x) =
-
x2
+ 2x
+
3 |
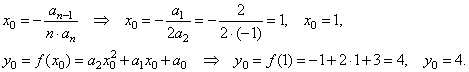 |
| 2)
To
get the source quadratic function, plug the coordinates
of translations (with changed signs) |
|
into the general form
of the quadratic, i.e., |
| y
+ y0
= a2(x
+ x0)2
+ a1(x
+ x0)
+ a0
=>
y
+ 4
= -
(x
+ 1)2
+ 2(x
+ 1)
+
3 |
|
y
=
-
x2
the source quadratic function |
| 3)
Inversely, by plugging the coordinates of translations into the source quadratic function |
| y
- y0
= a2(x
- x0)2
=>
y
- 4
= -
(x -
1)2
|
|
obtained is given quadratic in general form
y
=
-
x2
+ 2x
+
3. |
|
| Quadratic equation
word problems |
| Example:
A train made up for delay of 12 minutes after 60 km of way by running 10 km/h faster then regular speed.
What is the regular speed of the train? |
|
|
|
| Example:
In a theater each row has the same number of seats. Number of rows equals number of seats. By doubling number
of rows and decreasing number of seats 10 per row, total number of seats in the theater increases by 300. How
many rows are in the theater? |
| Solution:
Taking x
as the number of rows (or
seats per row),
then |
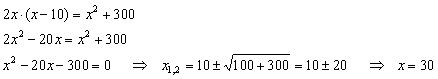 |
|
|
|
|
|
|
|
|
|
|
|
|
|
College
algebra contents C
|
|
 |
|
| Copyright
© 2004 - 2020, Nabla Ltd. All rights reserved. |