|
|
|
| Polynomial and/or Polynomial
Functions and Equations |
Roots or zeros of
polynomial function |
|
Graphing
polynomial functions |
|
Zero polynomial |
|
Constant function |
|
Linear function |
|
Quadratic function
and equation |
|
|
|
|
|
|
| Roots or zeros of
polynomial function |
| The
zeros of a polynomial function are the values of x
for which the function equals zero. |
| That
is, the solutions of the equation f
(x)
= 0,
that are called roots of the polynomial, are the zeros of the
polynomial function or the x-intercepts of its
graph in a coordinate plane. |
| At
these points the graph of the polynomial function cuts or
touches the x-axis. |
| If
the graph of a polynomial intersects with the x-axis
at (r,
0), or x
= r
is a root or zero of a polynomial, then (x
-
r)
is a factor of that polynomial.
|
| Every
polynomial of degree n
has exactly n
real and/or complex zeros. |
| An
nth
degree polynomial has at most n
real zeros. |
| Some
of the roots may be repeated. The number of times a root is
repeated is called multiplicity or
order of the root. |
| The
number ri
is a root of the
polynomial f
(x)
if and only if
f (x)
is divisible by
(x
-
ri).
|
| Therefore,
a polynomial and/or polynomial
function with
real coefficients can be expressed as a product of its leading
coefficient an
and
n
linear factors of the form (x
- ri),
where ri
denotes its real root and/or complex root, |
| f
(x)
= anxn
+ an-1xn-1
+
.
. .
+
a1x
+ a0
= an(x
- r1)(x
- r2)
.
. . (x
- rn).
|
| Thus, finding the roots of a
polynomial f(x)
is equivalent to finding its
linear divisors or is equivalent to polynomial
factorization into
linear factors. |
|
| Graphing
polynomial functions |
| Polynomial
functions are named in accordance to their degree. |
| Zero polynomial |
| The
constant polynomial f
(x)
= 0
is called the zero polynomial and
is graphically represented by the x-axis. |
| Constant function |
| A
polynomial of degree 0, f
(x)
= a0,
is called a constant function,
its
graph is a horizontal line with y-intercept
a0. |
 |
|
| Linear function |
| The
polynomial function of the first degree, f
(x)
= a1x
+ a0, is called a linear function. |
 |
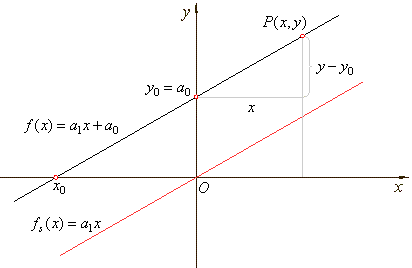| Since
y
= f (x) then
|
y
= a1x
+ a0
or y
= a1(x
-
x0)
or y
-
y0
= a1x, |
|
|
| where |
 |
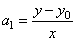is the slope
of the linear function, |
|
| and
where |
 |
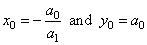are the coordinates
of translations of the linear function. |
|
|
| by
setting x0
= 0 or
y0
= 0, we
get y
= a1x,
the source linear function. |
|
| Quadratic function
and equation |
| The
polynomial function of the second degree, f
(x)
=
a2x2
+ a1x
+ a0, is called a
quadratic function. |
 |
| |
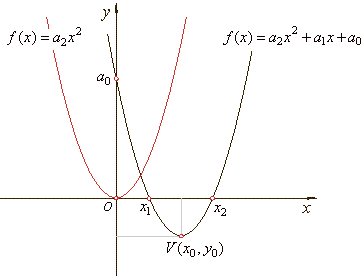y
= f (x)
=
a2x2
+ a1x
+ a0 or
y
-
y0
= a2(x
-
x0)2, |
where |
|
 |
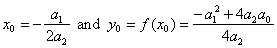coordinates
of translations of the quadratic function. |
|
| By
setting x0
=
y0
= 0, we get |
y
=
a2x2,
the source quadratic function.
The turning point V
(x0,
y0). |
|
| The
real zeros of the
quadratic function: |
 |
|
| |
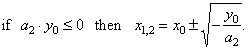y
= f (x) =
a2x2
+ a1x
+ a0 = a2(x
- x1)(x
- x2)
= a2[x2
-
(x1 +
x2)x
+
x1x2] |
|
| The graph of a quadratic function is curve called a parabola. The parabola is symmetric with respect to a vertical line
called the axis of symmetry. |
| As
the axis of symmetry passes through the vertex of the parabola
its equation is x
= x0. |
|
|
|
|
|
|
|
|
|
|
|
|
|
College
algebra contents C
|
|
 |
|
| Copyright
© 2004 - 2020, Nabla Ltd. All rights reserved. |
