|
| Conic
Sections |
|
|
|
|
Conics, a Family of Similarly Shaped Curves
- Properties of Conics
|
Dandelin's
Spheres - proof of conic sections focal properties
|
|
Proof that conic section curve is the parabola
|
|
Conics - a family of similarly shaped curves |
|
|
|
|
|
|
| Dandelin's spheres proof that conic section curve is the parabola
|
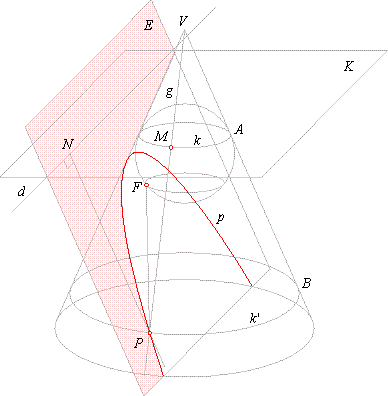
| When the cutting plane is parallel to any generator of one of the cones then we can insert only one sphere into
the cone which will touch the plane at the point F
and the cone surface at the circle
k.
|
|
Arbitrary chosen generating line
g
intersects the circle k
at a point
M,
and the intersection curve p
at a point
P.
The point P lies on the circle
k' which is
parallel with the plane K as shows
the down figure.
|
| By rotating the generator
g
around the vertex
V, the
point P
will move along the intersection curve.
|
|
While the generator approaches position to be parallel to the
plane
E, the point
P will move far away from
F.
That shows the basic property of the parabola that the line
at infinity is a tangent.
|
|
The segments,
PF
and PM
belong to tangents drawn from P
to the sphere
|
|
so, PM
= PF.
|
|
Since planes of the circles,
k
and k'
are parallel to each other and
perpendicular to the section through
the cone
axis, and as the plane E
is parallel to the slanting edge
VB, then
the intersection
d, of planes
E
and
K,
is also
perpendicular to the section
through the cone axis.
|
|
Thus, the perpendicular
PN from
P to
the line
d,
|
|
PN =
BA =
PM
or PF =
PN.
|
|
 |
|
|
Therefore, for any point
P
on the intersection curve the distance from the fixed point
F
is the same as it is from the fixed line
d, it proves that the intersection curve is the parabola.
|
|
| Conics - a family of similarly shaped curves |
| A conic is the set of points
P
in a plane whose distances from a fixed point F
(the focus) and a fixed line d
(the directrix), are in a constant ratio. This ratio named the
eccentricity e
determines the shape of the curve.
|
| We can see that conics represent a family of similarly shaped curves if we write their equations in vertex
form.
|
Recall the method we used to transform equations of the ellipse and the hyperbola from standard to
vertex form. We placed the vertex of the curve at the origin translating its graph.
|
|
Thus, obtained are their vertex
equations;
|
| y2 =
2px -
(p/a)x2 |
| -
the
ellipse
and the
circle |
| (for
the circle p =
a = r) |
|
|
|
|
| y2 =
2px + (p/a)x2 |
| -
the
hyperbola |
|
|
|
Using geometric interpretation of
these
equations we compare the area of the square
y2, formed by the ordinate of a
point
P(x,
y), with the
area of the rectangle
2p · x, whose
one side is the abscissa
x
of the point P
and the parameter 2p
other side, it follows that
|
|
 |
|
|
- for the ellipse the area of the square is smaller, than the area of the rectangle,
|
|
- for the parabola is equal,
|
|
- for the hyperbola the area of the square is greater than the area of the rectangle.
|
| The names of curves were given as a result of the above relations,
so; |
|
- the word “ellipse” (elleipyis)
in Greek means “deficiency," |
|
- the word “parabola” (parabolh)
means “equality” and |
|
- the word “hyperbola” (uperbolh)
means “excess.” |
|
| In
the given vertex equations we can make following substitutions for; |
|
- the ellipse |
 |
|
|
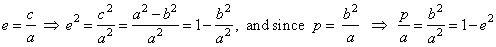- the
circle |
p =
a = b = r
=> e
= 0 |
|
|
|
|
- the
hyperbola |
 |
|
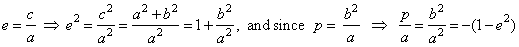| Thus, the
equation of conics in vertex form is |
y2 =
2px -
(1 -
e2)x2.
|
|
|
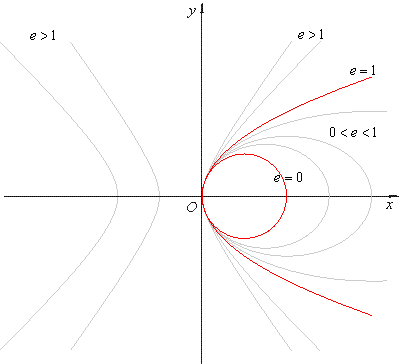
| The values of
e
define the curve the conic section makes, such that for |
|
e = 0
- a circle, |
|
0 < e < 1
- an ellipse, |
|
e = 1
- a parabola, |
|
e > 1
- a hyperbola, |
| as shows
the above figure. |
