|
|
Vectors in a Plane and Space |
|
|
|
|
|
Vectors
in a Plane |
 Vectors - introduction
Vectors - introduction |
|
Length, magnitude or
norm of the vector |
 Collinear, opposite
and coplanar vectors
Collinear, opposite
and coplanar vectors |
 Addition of vectors
Addition of vectors |
|
Triangle rule (law)
and parallelogram rule |
|
Zero or null vector |
|
|
|
|
|
|
| Vectors - introduction |
There are physical quantities like force, velocity, acceleration and others that are not fully determined by their
numerical data.
|
| For example, a numerical value of speed of motion, or electric or magnetic field strength, not
give us the information about direction it move or direction they act.
|
Such quantities, which are completely specified by a magnitude and a direction, are called vectors or vector
quantities and are represented by directed line segment. |
| Thus,
a vector is denoted as
|
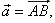 |
where the point
|
|
|
A is called the tail or start and point
B, the head or
tip.
|
| The length or magnitude or norm of the vector
a
or |
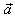 |
is |
|
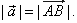
|
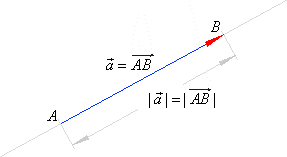
| Therefore, the length of the arrow represents the vector's magnitude, while
the direction in which the arrow points, represents the vector's direction. |
|
 |
|
| A vector with no magnitude, i.e., if the tail and the head coincide, is called the
zero or null vector
denoted |
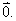 |
|
|
| Collinear, opposite
and coplanar vectors |
| Two vectors are said to be
equal if they have the same
|
| magnitude
and direction or if by parallel shift or
|
| translation one could be
brought into coincidence with
|
| the other, tail to tail and head to
head. |
|
 |
|
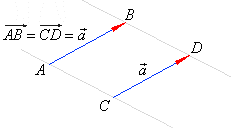
| Vectors are said to be
collinear if they lye on the same line or on
parallel lines.
|
|
| Vectors,
|
 |
in
the above figure are
collinear. |
|
| Two collinear vectors of the same magnitudes but opposite directions are said to be
opposite vectors. |
| A vector that is opposite to |
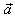 |
is
denoted |
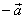 |
as shows the
above right figure. |
|
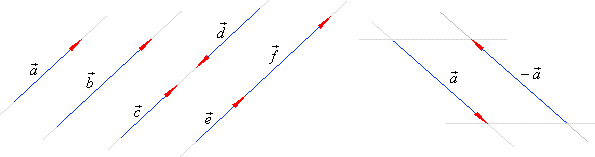
Three or more vectors are said to be
coplanar if they lie on the same plane. If two of three vectors are
collinear then these vectors are coplanar.
|
| To prove this statement, take vectors,
|
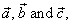 |
of which
|
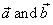 |
are
collinear.
|
|
|
By using translation bring the tails of all three vectors at the same point. Then, the common line of
vectors,
|
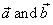 |
and the line in which lies the vector
|
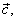 |
determine the unique plane. |
|
| Therefore, if vectors are
parallel to a given plane, then they are coplanar.
|
|
| Addition of vectors |
| The sum of vectors, |
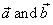 |
can be obtained graphically by placing the tail of |
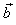 |
to the tip or head of |
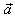 |
|
| using translation.
Then, draw an arrow from the initial point (tail) of |
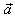 |
to the endpoint
(tip) of |
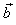 |
to obtain |
|
| the
result. |
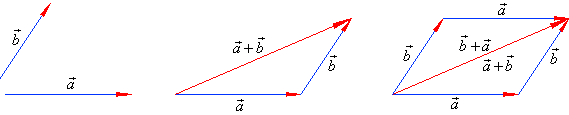 |
| The
parallelogram in the above figure shows the addition |
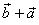 |
where, to the tip of |
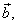 |
by translation, placed |
|
| is the tail of |
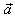 |
then, drawn
is the resultant |
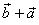 |
by joining the tail of |
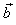 |
to the tip of |
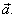 |
|
|
| Note that the tips of the resultant and the second summand should coincide. |
| Thus, in the above figure
shown is, the triangle
rule (law) and the parallelogram
rule for finding the
resultant or |
|
the addition of the two given vectors. The result is the same
vector, that is
|
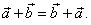 |
| Therefore, vector addition is commutative. |
| Since vectors, |
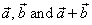 |
form a triangle, they lie on the same
plane, meaning they are coplanar. |
|
| |
| Addition of three vectors,
|
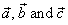 |
is defined as
|
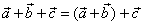 |
and represented graphically
|
|
|
|
| The
above diagrams show that vector addition is
associative, that is |
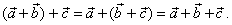 |
|
| The same way defined is the sum of four vectors. |
|
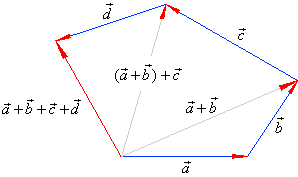 |
|
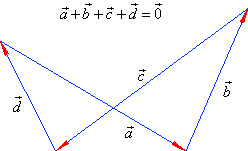
| If by adding vectors obtained is a closed polygon, |
|
then the sum is a null vector. |
 |
|
|
|
| By adding a vector |
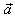 |
to its opposite vector |
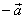 |
,
graphically it leads back to the initial point, therefore |
|
|
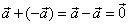 |
so, the
result is the null vector. |
|
|
|
|
|