|
| Conic
Sections |
|
|
|
|
Conics, a Family of Similarly Shaped Curves
- Properties of Conics
|
 Dandelin's
Spheres - proof of conic sections focal properties
Dandelin's
Spheres - proof of conic sections focal properties
|
|
Proof that conic section curve is
the ellipse
|
|
Proof that conic section curve is the hyperbola
|
|
|
|
|
|
|
| Conics, a
family of similarly shaped curves
- properties of conics |
|
By intersecting
either of the two right circular conical surfaces (nappes) with the plane perpendicular to the
axis of
the cone the resulting intersection is a circle
c, as
is shown in the figure. |
|
|
When the cutting plane is inclined to the axis of the cone at a greater angle than that made by
the generating segment or generator (the slanting edge of the cone), i.e., when the plane cuts all
generators of a single cone, the resulting curve is the
ellipse
e.
|
| Thus, the circle is a special case
of the ellipse in which the plane is perpendicular to the axis of the cone.
|
|
|
If the cutting plane is parallel to any generator of one of the cones, then the intersection curve is
the
parabola
p.
|
|
|
When the cutting plane is inclined to the axis at a smaller angle than the generator of the cone,
i.e., if the intersecting plane cuts both cones the
hyperbola
h
is generated.
|
|
 |
|
|
| Dandelin Spheres - proof of conic sections focal properties |
| Proof that conic section curve is
the ellipse
|
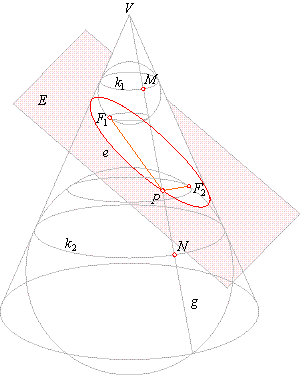
| In the case when the plane
E
intersects all generators of the cone, as in down figure, it is possible
to inscribe two spheres which will touch the conical surface and the plane. |
| Upper sphere touches the cone surface in a circle
k1
and the plane at a point F1.
Lower sphere touches the cone surface in a circle
k2
and the plane at a
point
F2.
|
Arbitrary chosen generating line g
intersects the
circle
k1
at a point
M, the circle
k2
at a point
N
and
the intersection curve e
at a point
P.
|
We see that points,
M
and F1
are the tangency
points of the upper sphere and points, N
and F2
the
tangency points of the lower sphere of the tangents
drawn from the point P
exterior to the spheres.
|
|
Since the segments of tangents from a point
exterior to sphere to the points of contact, are equal
|
|
PM =
PF1
and PN =
PF2.
|
|
And since planes of
circles k1and
k2,
are parallel, then are all corresponding generating segments
equal
|
|
MN =
PM +
PN
is constant.
|
|
Thus, the intersection curve is the locus of points
in the plane for which sum of distances from the two
fixed
points F1and
F2, is constant, i.e., the curve is
the ellipse.
|
|
 |
|
| The proof due to the French/Belgian mathematician Germinal Dandelin (1794 –
1847). |
|
| Proof that conic section curve is the hyperbola
|
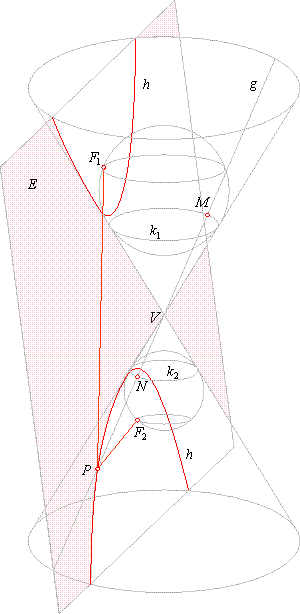
| When the intersecting plane is inclined to the vertical
axis at a smaller angle than does the generator of the
|
|
cone, the plane cuts both cones creating the
hyperbola
h which therefore consists of two disjoining
branches
as shows the
right figure.
|
|
Inscribed spheres touch the plane on the same side
at points
F1
and F2
and the cone surface at circles
k1and k2.
|
|
The generator
g
intersects the circles k1and k2, at
points, M and
N, and the intersection curve at the
point
P.
|
By rotating the generator
g
around the vertex V
by
360°,
the point P
will move around and trace both
branches of the hyperbola.
|
|
While rotating, the generator
will coincide with the plane two times and then will have common points
with the curve only at infinity.
|
|
As the line
segments, PF1and
PM are the tangents
segments drawn from P
to the upper sphere, and the segments PF2
and
PN
are the tangents segments drawn to the lower sphere, then
|
|
PM =
PF1
and PN =
PF2.
|
|
Since the planes of
circles k1
and k2, are parallel,
then are all generating segments from
k1to
k2
of equal
length,
so
|
|
MN =
PM -
PN
or PF1
-
PF2
is constant.
|
Thus, the intersection curve is the locus of points in
the plane for which difference of distances from the
two fixed
points F1
and F2, is constant, i.e., the curve is
the hyperbola.
|
|
 |
|
|
|
|
|
|
|
|
|
|
|
|
| College
algebra contents E |
|
 |
|
| Copyright
© 2004 - 2020, Nabla Ltd. All rights reserved. |
|
|