|
|
Power
series |
 Maclaurin and Taylor series
Maclaurin and Taylor series |
 The
binomial series
The
binomial series
|
|
The binomial
series expansions to the power series
|
|
The binomial
series expansion to the power series example
|
|
|
|
|
|
|
| Maclaurin and Taylor series |
| Consider
the polynomial function |
|
f (x) = an
xn
+ an -
1 xn -
-
1 + · · · + a3 x3
+ a2 x2 + a1 x
+ a0.
|
| If
we write the value of the function and the values of its successive
derivatives, at the origin, then |
| f
(0) =
a0, f '(0) = 1· a1,
f ''(0) = 1· 2a2,
f '''(0) = 1· 2· 3a3, . . . , f (n)
(0) =
n! an |
| so we
get the coefficients; |
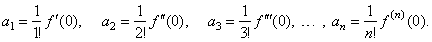 |
|
| Then,
the polynomial
f (x)
with infinitely many terms, written as the power series |
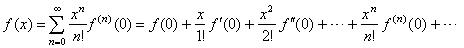 |
and |
|
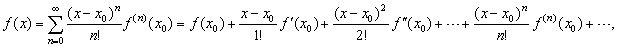 |
| where
0! = 1,
f (0) (x0)
= f
(x0)
and
f (n)
(x0) is the nth
derivative of f at
x0, |
|
represents an infinitely differentiable function
and is called Maclaurin series and Taylor series respectively. |
|
|
The
binomial series
|
|
We use the binomial theorem to expand
any positive integral power of a binomial (1
+ x)k,
as a polynomial with
k + 1
terms,
|
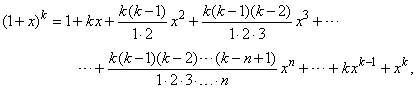
|
|
or
when writing the binomial coefficients in the shorter form
|
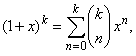
|
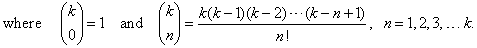
|
|
Assuming
f (x) =
(1
+ x)k,
where
k
is any real number, the function can be represented as a power
series using
the Maclaurin's formula,
|
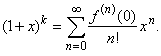
|
|
Therefore,
we should calculate f (0)
and evaluate its successive derivatives at x =
0
to write f
(n) (0),
so
|
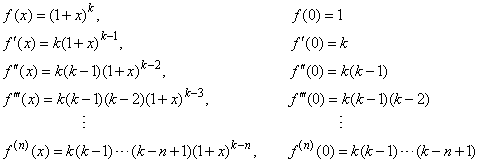
|
|
Thus,
the Maclaurin's series for the power function
|
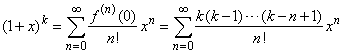
|
| or |
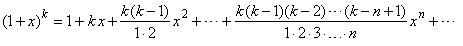 |
|
|
|
is
called the binomial series.
|
|
We
can use the ratio test to examine its convergence, as
|
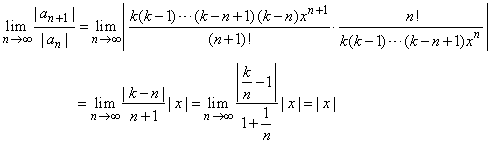
|
|
the binomial series
converges if | x
| < 1 and diverges if |
x | > 1.
|
|
Regarding
the endpoints, 1
and -1
of the interval of convergence, the series converges at 1
if -1
< k < 0
and
at both endpoints if k
> 0.
|
|
|
|
The binomial
series expansions to the power series
|
|
Hence,
for different values of k,
the binomial series
|
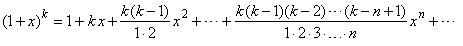
|
|
gives
the power series expansion of functions that we often use in
calculus, so
|
|
a)
for k
= -1
|
|
|
|
b)
for k
= -1/2
|
|
|
|
c)
for k
= 1/2
|
|
|
|
d)
for k
= 1/m
|
|
|
|
|
|
The binomial
series expansion to the power series example
|
| Let's
graphically represent the power series of one of the above
functions inside its interval
of convergence. |
|
| Example: Represent
f (x)
= 1/(1 + x2)
by the power series
inside the interval of convergence, graphically. |
| Solution: As
the sum of a power series is a function, the domain of which is
the set of those values of x
for which the series converges to the value of the
function then, |
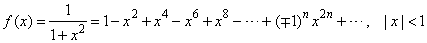 |
| let
write down the initial sequence of nth
order polynomials that describe the function inside the interval of convergence
-1
< x < 1, |
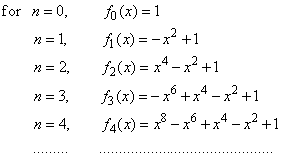 |
| Since
every polynomial above is missing the preceding odd degree term, their
coefficient an-1
= 0 |
| thus, the coordinates
of translations |
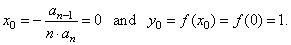 |
|
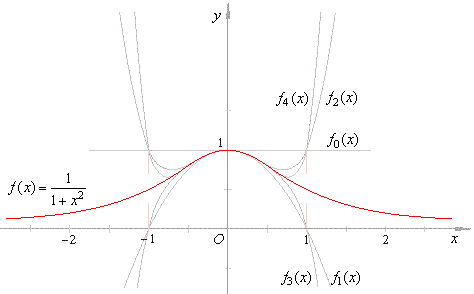
| Therefore,
the polynomials that describe the function
all are
source polynomials of even degree translated in the
direction
of the y
axis by y0
= 1, as is shown in the picture below.
|
|
| The above graph shows, all evenly indexed polynomials, with the positive
leading coefficient, intersect at (-1,
1) and (1,
1) while all polynomials with odd
indexes, with the negative leading coefficient, intersect at (-1,
0) and (1,
0). |
| Thus, they will never reach the
functions values f
(-1)
= 1/2 and f
(1) = 1/2, though their graphs
come closer and closer to the points (-1,
1/2) and (1, 1/2) as n
increases. |
|
|