|
|
Power
series |
Maclaurin and Taylor series |
|
The power series expansion of the hyperbolic sine and hyperbolic cosine function |
|
Properties
of the power series expansion of the hyperbolic sine and hyperbolic cosine function |
|
|
|
|
|
|
| Maclaurin and Taylor series |
| Consider
the polynomial function |
|
f (x) = an
xn
+ an -
1 xn -
1 + · · · + a3 x3
+ a2 x2 + a1 x
+ a0.
|
| If
we write the value of the function and the values of its successive
derivatives, at the origin, then |
| f
(0) =
a0, f '(0) = 1· a1,
f ''(0) = 1· 2a2,
f '''(0) = 1· 2· 3a3, . . . , f (n)(0) =
n!an |
| so we
get the coefficients; |
 |
|
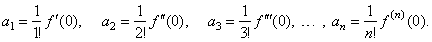| Then,
the polynomial f (x)
with infinitely many terms, written as the power series |
 |
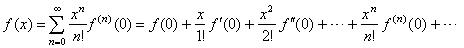and |
|
 |
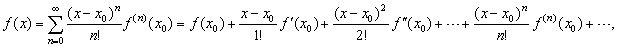| where
0! = 1,
f (0) (x0)
= f
(x0)
and
f (n)
(x0)
is the nth
derivative of f at
x0, |
|
represents an infinitely differentiable function
and is called Maclaurin series and Taylor series respectively. |
|
| The power series expansion of the
hyperbolic sine and hyperbolic cosine function |
| We
use sum and difference of two convergent series |
 |
| to
represent the
hyperbolic sine (sinh
or sh)
and hyperbolic cosine (cosh
or ch)
function by the power series. |
| Since, |
 |
|
|
 |
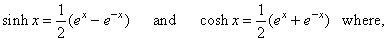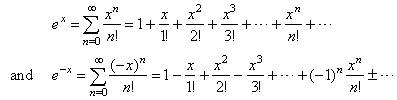| then, |
 |
|
|
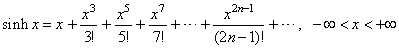| and |
 |
|
|
|
|
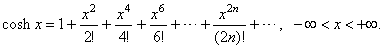Properties
of the power series expansion of the hyperbolic sine and hyperbolic cosine function |
| The
hyperbolic sine |
|
|
|
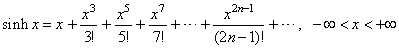| The
hyperbolic sine is represented by the infinite polynomial lacking every
next even term so that an-1
= 0 |
| therefore, the
coordinates of translations, |
 |
|
|
 |
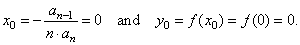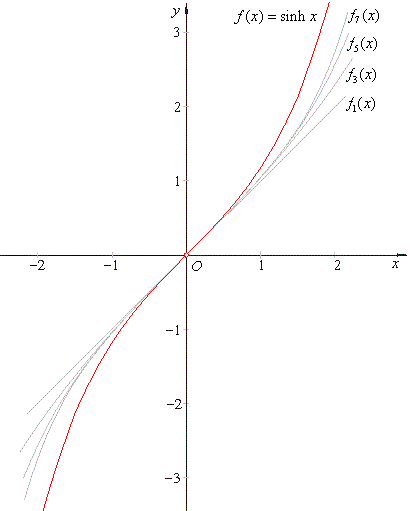| Thus, the infinite
source odd polynomials describe the graph of the hyperbolic
sine, |
 |
|
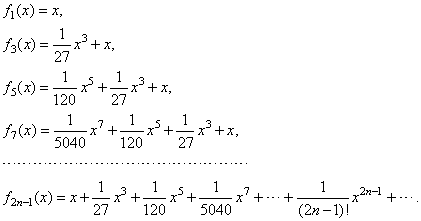| The
hyperbolic cosine |
|
|
|
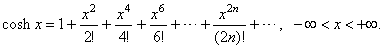| The
hyperbolic cosine is represented by the infinite polynomial lacking every
next odd term so that an-1
= 0 |
| therefore, the
coordinates of translations, |
 |
|
|
 |
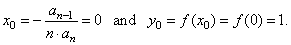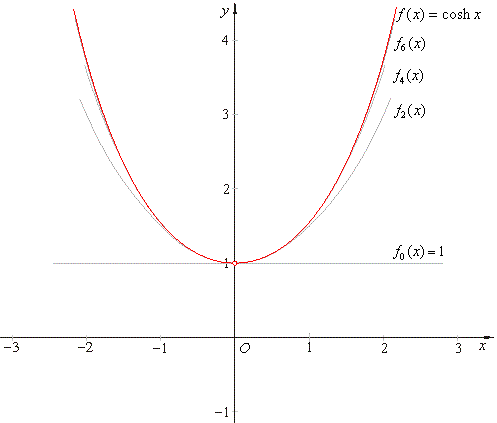| Thus,
the infinite source even polynomials translated by y0
= 1 describe the graph of the hyperbolic
cosine, |
 |
|
|
|
|
|
|
|
|
|
|
|
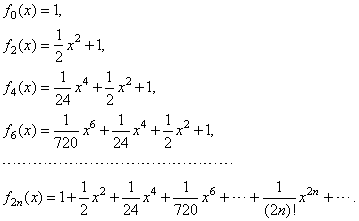| Calculus
contents B |
|
 |
|
| Copyright
© 2004 - 2020, Nabla Ltd. All rights reserved. |
|
|
