|
A limit
on the left (a left-hand limit) and a limit
on the right (a right-hand limit) |
|
Continuous
function |
|
Limits
at infinity (or limits of functions as x approaches
positive or negative infinity) |
|
Infinite limits |
|
The
limit of a function examples |
|
Vertical, horizontal
and slant (or oblique) asymptotes |
|
|
|
|
|
|
| The
definition of the limit of a function |
| The
limit of a function is a real number L
that f
(x)
approaches as x
approaches a given real number a,
written |
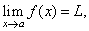 |
| if
for any e
> 0 there is a d(e)
> 0 such that
|
f
(x)
-
L | < e
whenever | x
-
a | < d(e). |
| The
definition says, no matter how small a positive number e
we take, we can find a positive number d
such that, for an arbitrary chosen value of x
from
the interval a
-
d
< x
< a +
d,
the corresponding function's values lie inside
the interval |
|
L
-
e
< f
(x)
< L +
e, |
|
as shows the right figure. |
| That
is, the function's values can be made arbitrarily
close to the number L
by choosing x
sufficiently
close to
a, but not equal to
a. |
|
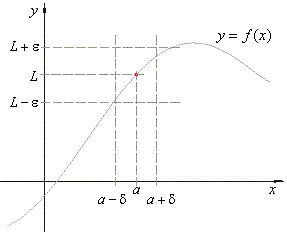 |
|
| Therefore,
the number d,
that measures the distance between a point x
from the point a
on the x-axis,
depends
on the number e
that measures the distance between the point f
(x)
from the point L
on the y-axis. |
| Example: Given |
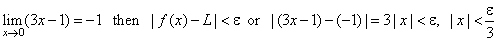 |
|
|
whenever |
 |
|
| A
limit is used to examine the behavior of a function near a point
but not at the point. The function need not even be defined at
the point. |
|
| A
limit on the left (a left-hand limit) and a limit
on the right (a right-hand limit) |
| The
limit of a function where the variable x
approaches the point a
from the left or, where x
is restricted to values
less than a,
is written |
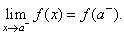 |
| The
limit of a function where the variable x
approaches the point a
from the right or, where x
is restricted to values
grater than a,
is written |
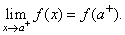 |
| If
a function has both a left-handed limit and a right-handed limit
and they are equal, then it has a limit at the point. Thus,
if |
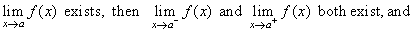
|
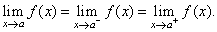 |
|
| Continuous
function |
| A
real function
y = f (x)
is continuous at a point a
if it is defined at x =
a
and |
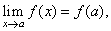 |
| that
is, if for every e
> 0 there is a d(e)
> 0 such that |
f
(x)
-
f
(a)
| < e
whenever | x
-
a | < d (e). |
| Therefore,
if a function changes gradually as independent variable changes,
so that at every value a,
of the independent
variable, the difference between f
(x)
and f
(a)
approaches zero as x
approaches a. |
| A
function is said to be continuous if it is continuous at all
points. |
|
| Limits
at infinity (or limits of functions as x approaches
positive or negative infinity) |
| We
say that the limit of f(x)
as x
approaches positive infinity is L
and write, |
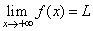 |
|
if for any e
> 0 there exists N
> 0 such that
|
f
(x)
-
L | < e
for all x
> N
(e). |
| We
say that the limit of f
(x)
as x
approaches negative infinity is L
and write, |
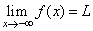 |
|
if for any e
> 0 there exists N
> 0 such that
|
f
(x)
-
L | < e
for all x
< -N
(e). |
|
| Not
all functions have real limits as x
tends to plus or minus infinity. |
| Thus
for example, if f
(x)
tends to infinity as x
tends to infinity we write |
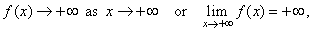 |
| if
for every number N
> 0 there is a number M
> 0 such that f
(x)
> N
whenever x
> M(N). |
|
| Infinite limits |
| We
write |
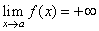 |
| if
f (x) can
be made arbitrarily large by choosing x
sufficiently close
but not equal to a. |
| We
write |
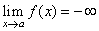 |
| if
f(x) can
be made arbitrarily large negative by choosing x
sufficiently close
but not equal to a. |
|
| The
limit of a function examples |
| Example: Evaluate
the following limits; |
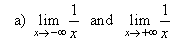 |
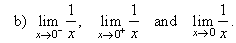 |
| Solution:
a) As x
tends to minus infinity f(x)
gets closer and closer to 0. |
| As x
tends to plus infinity f(x)
gets closer and
closer to 0. Therefore, |
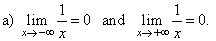 |
| b) As x
tends to 0 from the left f(x)
gets larger in negative sense. |
|
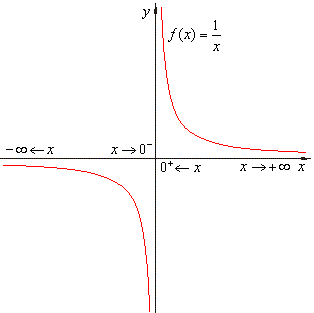 |
|
| As
x
tends to 0 from the right f(x)
gets larger in positive sense. Therefore, |
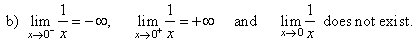 |
|
| Vertical, horizontal
and slant (or oblique) asymptotes |
| If
a point (x, y) moves
along a curve f
(x)
and then at least one of its coordinates tends to infinity,
while the distance between the point and a line tends to zero
then, the line is called the asymptote
of the curve. |
|
| Vertical
asymptote |
| If
there exists a number a
such that |
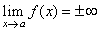 |
| then
the line x
= a is the vertical
asymptote. |
|
| Horizontal
asymptote |
| If
there exists a number c
such that |
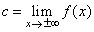 |
| then
the line y
= c is the horizontal
asymptote. |
|