|
|
Power
series |
Maclaurin and Taylor series |
|
The power series expansion of the logarithmic function |
|
Properties
of the power series expansion of the logarithmic function |
|
|
|
|
|
|
| Maclaurin and Taylor series |
| Consider
the polynomial function |
|
f (x) = an
xn
+ an -
1 xn -
-
1 + · · · + a3 x3
+ a2 x2 + a1 x
+ a0.
|
| If
we write the value of the function and the values of its successive
derivatives, at the origin, then |
| f
(0) =
a0, f '(0) = 1· a1,
f ''(0) = 1· 2a2,
f '''(0) = 1· 2· 3a3, . . . , f (n)
(0) =
n! an |
| so we
get the coefficients; |
 |
|
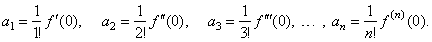| Then,
the polynomial
f (x)
with infinitely many terms, written as the power series |
 |
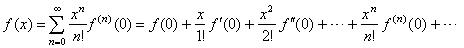and |
|
 |
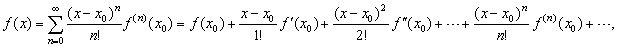| where
0! = 1,
f (0) (x0)
= f
(x0) and
f (n)
(x0) is the nth
derivative of f at
x0, |
|
represents an infinitely differentiable function
and is called Maclaurin series and Taylor series respectively. |
|
|
The power series expansion of the logarithmic function |
| Example: Let
represent the translated (shifted) logarithmic function f
(x)
= ln (x + 1)
by the power series. |
| Solution: Given
translated logarithmic function is the infinitely differentiable function defined
for all |
|
-
1 < x < oo
. We use the polynomial
with infinitely many terms in the form of power series
|
 |
|
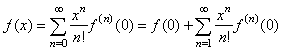to represent given function. We
should calculate the function value f
(0),
and some successive derivatives of
|
|
the logarithmic
function, to determine the nth
order derivative.
|
 |
|
|
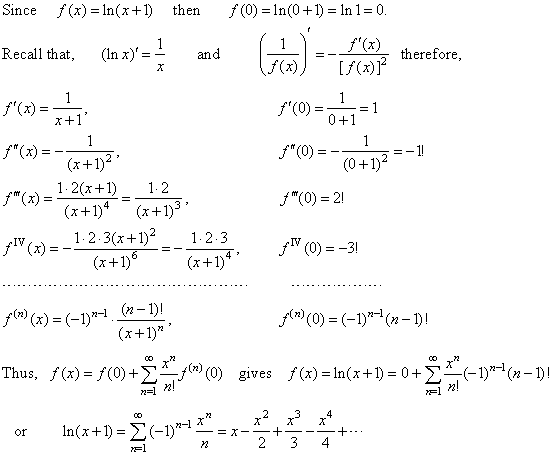Properties
of the power series expansion of the logarithmic function |
| To
graphically represent the power series (or polynomial) expansion of the logarithmic function
we first calculate
the coordinates of translations of the given sequence of polynomials.
Since,
|
|
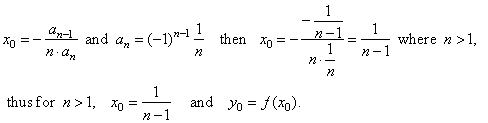
| The
sequence of the polynomials and
corresponding translations are written below |
 |
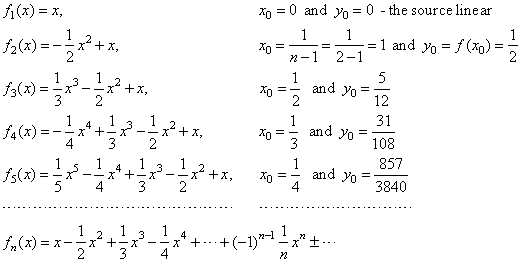| and
in the picture below shown are their graphs, where are also marked the (x0,
y0) points that
approach the origin
as n
tends to infinity. |
 |
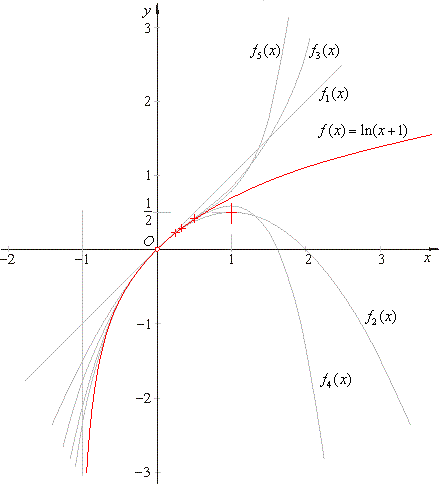| Inside
the interval -1
< x < 1 the graphs
of the polynomials approach closer and closer to the logarithmic function,
as n
increases, but for x
> 1
the graphs of even and odd degree
polynomials separate as shows
the picture above. |
| By
plugging the coordinates of translations with changed signs into the
polynomial expressed in the general form, we get the source polynomial
function. Thus, the source functions
of the above polynomials are |
 |
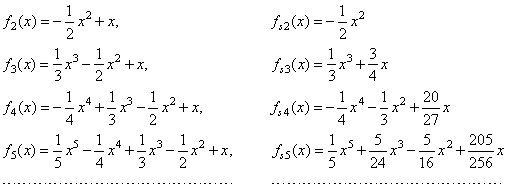| We
can apply the ratio test to check the interval of
convergence. |
| Since
the power series converges at every point x
from the open interval | x |
< r or -
r < x < r
and diverges for all
x outside this interval, where |
 |
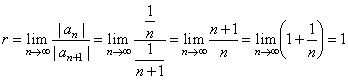| therefore
| x |
< r, | x |
< 1 or
the power series converges in the open interval -
1 < x < 1, and diverges
outside
this interval. |
| To
determine whether the power series converge or diverge at endpoints we
should plug each endpoint into the
given series and apply appropriate test for convergence. |
| The
f
(x)
= ln (x + 1) is not defined at x
= -1,
so we only test for convergence the right side endpoint by plugging
it into given power series. |
