|
|
|
|
|
|
|
| The
graphs of the
polynomial functions |
| The
polynomial function
f (x) =
y = anxn
+ an-1xn-1
+ an-2xn-2
+
.
. . +
a2x2
+
a1x + a0 |
| The
graph of a function ƒ
is drawing on the Cartesian plane, plotted with respect to
coordinate axes, that shows functional relationship between
variables. The points (x,
ƒ(x)) lying on the curve
satisfy this relation. |
|
| The
source
or original polynomial function |
| Any
polynomial f (x)
of degree n >
1 in the general form, consisting
of n
+ 1 terms, shown graphically, represents translation of its
source (original) function in the direction of the coordinate
axes. |
|
The source polynomial function |
|
fs(x)
= anxn
+ an-2xn-2
+
.
. . +
a2x2
+ a1x
|
|
|
| has
n
- 1 terms
lacking second and the constant term, since its coefficients, an-1
=
0
and a0
=
0
while
the leading coefficient an,
remains unchanged. |
| Therefore,
the source polynomial function passes through the
origin. |
| A
coefficient ai
of
the source function is expressed by the coefficients of the general
form. |
|
| Translating
(parallel shifting) of the polynomial function |
| Thus,
to obtain the graph of a given polynomial function f
(x)
we translate (parallel shift)
the
graph of its source function in the direction of the x-axis
by x0
and in the direction of the y-axis
by y0. |
| Inversely,
to put a given graph of the polynomial function beck to the
origin, we translate it in the opposite direction, by taking the
values of the
coordinates of translations with opposite sign. |
|
| Coordinates of translations
and their role in the polynomial expression |
| The
coordinates of translations we calculate using the formulas, |
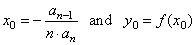
|
| Hence,
by plugging the coordinates of translations into
the source polynomial function fs(x),
i.e., |
|
y
- y0
= an(x
- x0)n
+ an-2(x
- x0)n-2
+
.
. .
+
a2(x
- x0)2
+ a1(x
- x0) |
|
|
| and
by expanding above expression we get the polynomial function in
the general form |
| f
(x) =
y = anxn
+ an-1xn-1
+ an-2xn-2
+
.
. . +
a2x2
+
a1x + a0. |
| Inversely, by plugging the coordinates of translations into
the given polynomial f
(x)
expressed in the general form,
i.e., |
|
y
+ y0
= an(x
+ x0)n
+ an-1(x
+ x0)n-1
+
.
. .
+ a1(x
+ x0)
+ a0 |
|
|
| and
after expanding and reducing above expression we get its source polynomial function. |
| Note
that in the above expression the signs of
the coordinates of translations are already changed. |
|
| Translated
monomial (or
power) function |
| If
we set all coefficients, an-2
to a1,
in the above expanded form of the
polynomial to zero, we get |
| y
- y0
= an(x
- x0)n,
x0
= -
an-1/(
n · an)
and y0
=
f
(x0). |
| the
translated
power (or monomial) function, the exponent of which is an odd or
an even positive integer. |
| When
the exponent is even, i.e., of the form n
= 2m,
m Î N,
the graph of the source power function y
= anxn
is symmetric about the y-axis,
that is f (-x)
=
f (x). |
| When
the exponent is odd, i.e., of the form n
= 2m
+ 1,
m Î N,
the graph of the source power function y
= anxn
is symmetric about the origin, that
is f (-x)
=
- f
(x). |
|
|
|