|
|
|
|
|
|
|
| The
graphs of the
polynomial functions |
| Translating
or parallel shifting the polynomial function |
| Thus,
to obtain the graph of a given polynomial function f
(x)
we translate (parallel shift)
the
graph of its source function in the direction of the x-axis
by x0
and in the direction of the y-axis
by y0. |
| Inversely,
to put a given graph of the polynomial function beck to the
origin, we translate it in the opposite direction, by taking the
values of the
coordinates of translations with opposite sign. |
|
| Coordinates of translations
and their role in the polynomial expression |
| The
coordinates of translations we calculate using the formulas, |
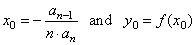
|
| Hence,
by plugging the coordinates of translations into
the source polynomial function fs(x),
i.e., |
|
y
- y0
= an(x
- x0)n
+ an-2(x
- x0)n-2
+
.
. .
+
a2(x
- x0)2
+ a1(x
- x0) |
|
|
| and
by expanding above expression we get the polynomial function in
the general form |
| f
(x) =
y = anxn
+ an-1xn-1
+ an-2xn-2
+
.
. . +
a2x2
+
a1x + a0. |
| Inversely, by plugging the coordinates of translations into
the given polynomial f
(x)
expressed in the general form,
i.e., |
|
y
+ y0
= an(x
+ x0)n
+ an-1(x
+ x0)n-1
+
.
. .
+ a1(x
+ x0)
+ a0 |
|
|
| and
after expanding and reducing above expression we get its source polynomial function. |
| Note
that in the above expression the signs of
the coordinates of translations are already changed. |
|
| Coefficients
of the source polynomial function are related to its derivative
at x0 |
| The
coefficients of the source polynomial are related to
corresponding value of its derivative at x0
like the coefficients
of the Taylor polynomial in Taylor's or Maclaurin's formula,
thus |
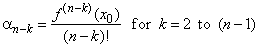 |
| where, an
= an,
an
-
1
= 0,
a0
= f (x0),
and where f
(n -
k)
(x0)
denotes (n -
k)th
derivative at x0. |
|
| Such
for example, the coefficient a1
of the source cubic of
f (x) =
a3x3
+
a2x2
+
a1x + a0 |
| since
f ' (x)
=
3a3x2
+ 2a2x
+
a1
and x0
=
-
a2/(3a3)
then |
 |
| Thus,
if y
= a4x4
+ a3x3
+
a2x2
+
a1x + a0
or y
-
y0
=
a4(x
-
x0)4
+
a2(x
-
x0)2
+
a1(x
-
x0), |
| where |
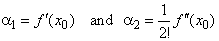 |
or
f
' (x0)
= 1!
a1
and f
'' (x0)
= 2!
a2 |
|
|
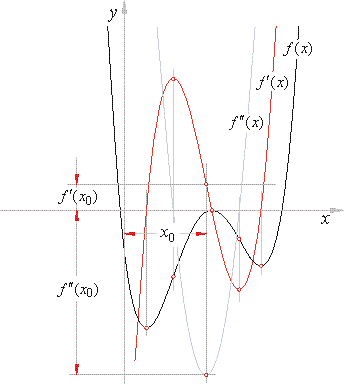
then,
a1
and
a2
define vertical translations of
the successive derivatives, as shows below figure.
|
 |
|