|
|
Applications
of differentiation - the graph of a function and its derivative |
 The mean value theorem
The mean value theorem |
|
Generalization
of the mean value theorem
|
|
Cauchy's mean value theorem or generalized mean value theorem |
|
|
|
|
|
|
|
| The
mean value theorem |
| If a function f
is continuous on a closed interval [a,
b]
and differentiable between its endpoints, then
there is a point c
between a
and b
at which the slope of the tangent line to f
at c
equals the slope of the secant line through
the points (a,
f (a))
and (b,
f (b)), |
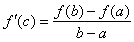 |
| as
shows the right figure above. |
| We
can also write the above formula as f
(b)
-
f (a) = f ' (c) (b -
a) |
|
and by substituting b
by x,
f
(x)
=
f (a) + f ' (c) (x -
a) |
|
|
Example:
Let
use the mean value theorem to prove that the abscissa of a point
of the parabola
|
|
f (x) = a2x2 + a1x
+ a0,
at
which the tangent is parallel to the secant line through
points (a,
f (a))
and |
| (b,
f (b)),
is
the midpoint of the interval [a,
b]. |
|
Solution:
Since the derivative of the parabola
f
' (x) = 2a2x + a1
then f
' (c) = 2a2c + a1,
and
|
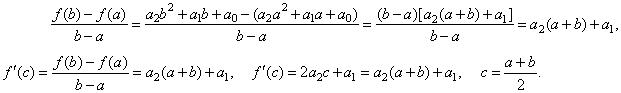 |
 |
|
| Generalization
of the mean value theorem |
| If
two functions,
f1
(x)
and f2
(x)
are continuous on a closed interval [a,
b]
and differentiable between its endpoints
have identical derivatives on that interval then they differ in a
constant. |
| That is, if
we write j
(x)
= f1
(x)
-
f2
(x),
then its derivative
j
'
(x)
= f1'
(x)
-
f2'
(x)
= 0 at every
point of
the
interval, therefore j
(x)
= constant
or |
| f1(x)
-
f2
(x)
= constant. |
| This
theorem we use in the integral calculus. |
|
|
Example: Given
is the derivative f
' (x) =
-
x2
-
8x
-
12 of a cubic function and
one of its roots x
=
-
1.
Find
the cubic and its source function and draw the graph of the cubic.
|
|
Solution:
Let factorize given quadratic to find its zeros,
|
| f
' (x) =
-
x2
-
8x
-
12 =
-
(x
+ 6)(x + 2),
x1
= -
6 and x2
= -
2 |
| and
calculate its translation in direction of the x-axis |
| x0
= -
an-1/(n
an),
(x0)n
= 2 = -
(-
8)/(2 · (-
1)) = -
4, (x0)n
= 2 = -
4. |
| Since,
a polynomial function and all its successive derivatives have the same
horizontal translation |
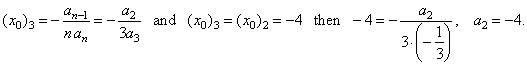 |
| Then,
we calculate coefficient a1
of the cubic |
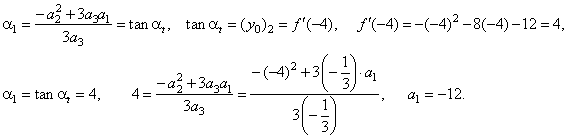 |
| where
a1 is the coefficient of the source cubic
fs(x) = a3x3 +
a1x
or fs(x) =
(-1/3)x3 +
4x. |
| Finally
we will find the coefficient a0
by plugging given x-intercept
(-1,
0) into the cubic |
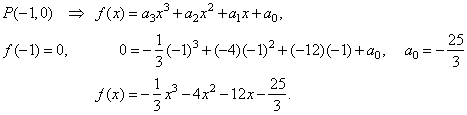 |
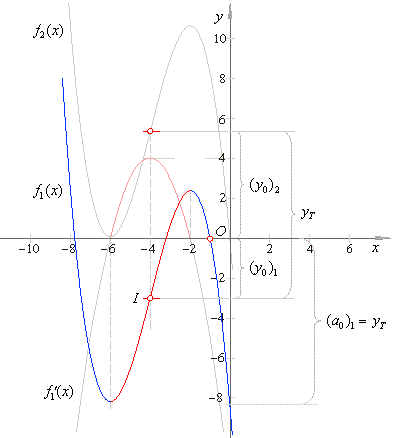
| The cubic
function and its derivative are shown in the figure below. |
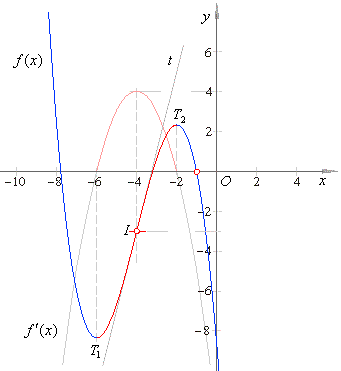 |
| Let
find translation of the graph of the cubic in direction of the y-axis
by plugging x0
= -
4
into its equation, |
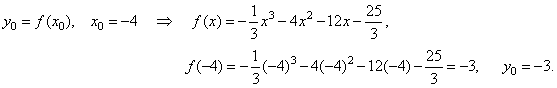 |
| Thus,
the graph of f
(x)
in the above figure is drawn translating the source cubic fs
(x) =
(-1/3)x3 +
4x
in direction
of the coordinate axes to the inflection point I(x0,
y0)
or I(-
4, -3). |
| To
check the source cubic expression mentioned above we should plug the coordinates
of translations, |
| x0
and y0
into y
+ y0
= a3(x
+ x0)3 +
a2(x + x0)2 +
a1(x + x0) +
a0, |
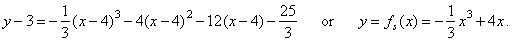 |
| Observe
that the problem can be solved almost straight considering we know how
find a function whose derivative
is given. The function we should find is called an antiderivative. |
| Therefore,
to determine whether a function f
(x)
is
an antiderivative, we simply differentiate it and check if the result
is equal to given f
' (x). |
| Let
denote f1(x)
the cubic we solved and
differentiate it |
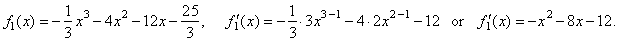 |
| Now,
let's do reverse, integrate ( or antidifferentiate) f1' (x), to return back the cubic |
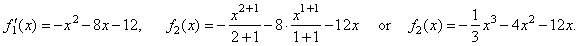 |
| Note
that the cubic functions, f1(x)
and
f2(x)
have the same derivatives and only differ in the constant term,
as was stated by the generalization of the mean value theorem above. |
| The
graph of f2(x),
the cubic missing the constant
term, passes through the origin. Therefore, we get its graph
by translating the graph of the cubic f1(x), in the positive direction
of
the y-axis
by
25/3,
which is shown in the below
figure. |
 |
| Proof,
both
functions f1
(x)
and
f2
(x)
have
the same translation x0
and the absolute value of the difference (
y0)1 -
(
y0)2
of the translations in direction of the y-axis
equals
25/3.
That is, |
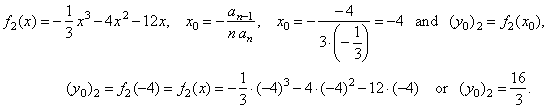 |
| Thus,
the source function of f2 |
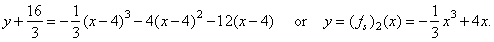 |
| Therefore, |
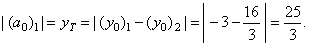 |
| Note,
that is why we should always add a constant C
to an antiderivative function as the substitution for the constant term lost by
differentiation. |
| Let's mention here yet another straight method, that is
on some way related to what was just shown above, known as Maclaurin's
formula or theorem. |
| An n-th
degree polynomial Pn
(x) =
anxn + an -
1xn -
1 + ·
· · + a2x2
+ a1x + a0, |
| applying Maclaurin's
theorem,
can be written as |
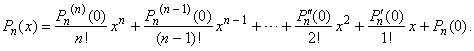 |
| Thus,
using Maclaurin's
formula we
can calculate coefficients of a polynomial
by evaluating all its successive derivatives
at the origin to the n-th
order. |
| Therefore,
we can find the coefficients of the cubic given in the
above example,
except the last term a0. |
|
Since given
is, P3' (x) =
-
x2
-
8x
-
12
then P3' (0) =
-12 |
|
P3'' (x) =
-
2x
-
8,
P3'' (0) =
-
8 |
|
and
P3''' (x) =
-
2,
P3'''
(0) =
-
2 |
| then
by
plugging obtained values into above Maclaurin's
formula |
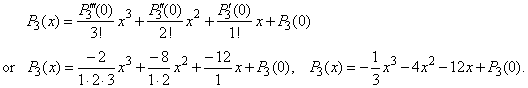 |
|
| Cauchy's mean value theorem
or generalized mean value theorem |
| If
f (x)
and g (x)
are differentiable in an interval (a,
b) and
continuous on [a,
b],
then |
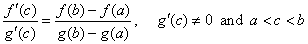 |
|
or f
' (c) [g (b)
-
g
(a)]
=
g' (c) [f (b)
-
f
(a)],
a
< c < b. |
| To
prove the above formula let |
| j
(x)
= f (x) [g (b)
-
g
(a)]
-
g (x) [f (b)
-
f
(a)] |
| then,
by calculating j
(a)
and j
(b)
we get |
| j
(a)
=
j
(b)
=
f (a) g (b) -
g (a)
f (b) |
| thus,
j
(x)
satisfies Rolle's theorem. |
| Therefore,
there exists at least one point c
in the interval (a,
b) such
that |
|
j'
(c)
= f ' (c) [g (b)
-
g
(a)]
-
g' (c) [f (b)
-
f
(a)]
= 0,
|
| what
proves the theorem. |
|
|
|
|