|
|
|
|
Applications
of differentiation - the graph of a function and its derivative |
 Definition
of increasing and decreasing
Definition
of increasing and decreasing |
|
Increasing/decreasing
test |
 Rolle's theorem
Rolle's theorem
|
 The mean value theorem
The mean value theorem |
|
|
|
|
|
|
| Definition
of increasing and decreasing |
| A
function f
is increasing on an interval I
if f (x1)
< f (x2)
for each x1
< x2 in I
. |
| A
function f
is decreasing on an interval I
if f (x1)
> f (x2)
for each x1
< x2 in I
. |
| Note
that we always examine the graph of a function moving from left to right (x1
< x2)
when determining the intervals
in which the function increases or decreases. |
|
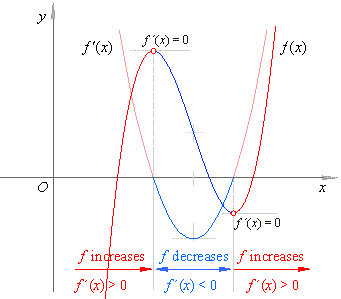
| Increasing/decreasing
test |
| If
the first derivative of a function f
is positive for all x
in an interval, then f
is increasing on that interval. |
| If
the first derivative of a function f
is negative for all x
in an interval, then f
is decreasing on that interval. |
 |
|
| Rolle's
theorem |
| If a
function f
is continuous on a closed interval [a,
b]
and differentiable between
a
and b,
for which the function
has the same value, that is f
(a)
= f (b),
then there exists point
c
inside the interval at which f
' (c) = 0,
as shows the left figure below. |
|
|
|
| The
mean value theorem |
| If a function f
is continuous on a closed interval [a,
b]
and differentiable between its endpoints, then
there is a point c
between a
and b
at which the slope of the tangent line to f
at c
equals the slope of the secant line through
the points (a,
f (a))
and (b,
f (b)), |
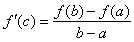 |
| as
shows the right figure above. |
| We
can also write the above formula as f(b)
-
f(a) = f ' (c)(b -
a) |
|
and by substituting b
by x,
f(x)
=
f(a) + f ' (c)(x -
a) |
|
|
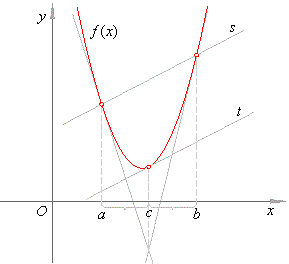
Example:
Let
use the mean value theorem to prove that the abscissa of a point
of the parabola
|
|
f (x) = a2x2 + a1x
+ a0,
at
which the tangent is parallel to the secant line through
points (a,
f (a))
and |
| (b,
f (b)),
is
the midpoint of the interval [a,
b]. |
|
Solution:
Since the derivative of the parabola
f
' (x) = 2a2x + a1
then f
' (c) = 2a2c + a1,
and
|
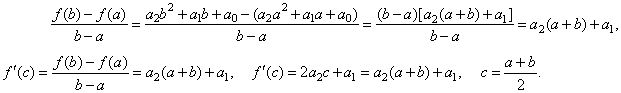 |
 |
|
|