|
|
Higher order derivatives and higher order differentials |
 Higher derivatives of parametric functions
Higher derivatives of parametric functions |
|
Higher derivatives of parametric functions examples |
 Higher order differentials
Higher order differentials |
|
Higher order differentials examples |
|
|
|
|
|
|
|
|
Higher derivatives of parametric functions |
| Assume
that f (t)
and g (t)
are differentiable and f
'(t) is not
0 then, given parametric curve can be
expressed as
y
= y (x) and this
function is differentiable at x,
that is |
|
x
= f (t)
or
t = f -1(x), |
|
by plugging
into y
= g (t)
obtained is y
= g [f -1(x)]. |
| Therefore,
we use the chain rule and the derivative of the inverse function to find
the first derivative of parametric
functions, |
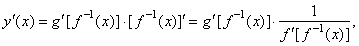 |
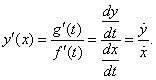 |
|
The second
derivative of parametric
functions, |
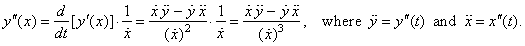 |
|
The
third derivative of parametric
functions, |
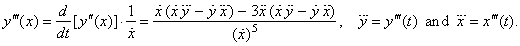 |
|
|
Higher derivatives of parametric functions examples |
|
Example:
Find
the second derivative of the parametric functions x
= ln t and
y
= t3
+ 1.
|
|
Solution:
Since |
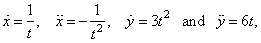 |
|
|
then, |
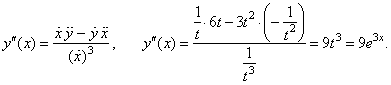 |
|
|
|
Example:
Find
the second derivative of the parametric functions |
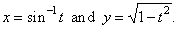 |
|
|
Solution:
Since |
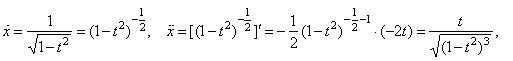 |
|
|
and |
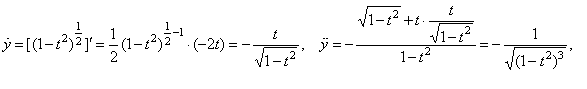 |
|
|
then, |
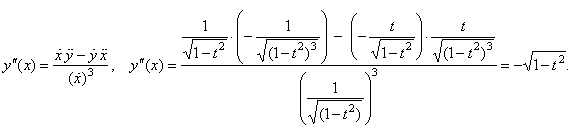 |
|
|
|
Higher order differentials |
| The
first order differential of a function y
= f (x)
at a point x |
| dy
= f '(x)dx = y'dx |
| is
defined as the linear part of the increment of the function expressed as
the product of the derivative of the function
and the corresponding increment of the independent variable. |
| The
second order differential is defined as the differential of the first
order differential with respect to the same increment dx,
written |
| d
2 y
= d (dy) = d (y'dx) = y'' (dx)2. |
| Similarly defined
are the third and the higher order differentials |
| d
3 y
= y''' (dx)3, |
| ·
·
·
·
·
·
·
·
·
· |
| ·
·
·
·
·
·
·
·
·
· |
| d
n y
= y (n) (dx)n. |
|
| Furthermore,
if y
= f (u), where
u = g
(x),
then |
| d
2 y
= y'' (du)2 +
y' d
2 u, |
| d
3 y
= y''' (du)3 +
3 y''
du d 2 u
+
y' d
3 u,
etc. |
| Note
that, here primes denote derivatives with respect to u. |
|
|
Higher order differentials examples |
|
Example:
Find
d
2 y
of the function y
= cos 3x.
|
|
Solution:
Therefore, given y
= f (u)
= cos
u,
where
u
= g (x)
= 3x.
|
| The
second differential we calculate using the formula |
|
d
2 y
= y'' (du)2 +
y' d
2 u,
where d
2 u
= g'' (x) (dx)2. |
| Since,
y' (u)
=
-
3sin
3x
then, y''
(u)
=
-
9cos
3x |
| and
g' (x)
= (3x)'
= 3
then, g''
(x)
= 0,
so that d
2 u
= 0. |
|
Thus, d
2 y
= -
9cos
3x
(du)2. |
| |
|
Example:
Find
d
2 y of the
function y
= sin x
· ln x.
|
|
Solution:
The second differential d
2 y
= y'' (dx)2,
since
|
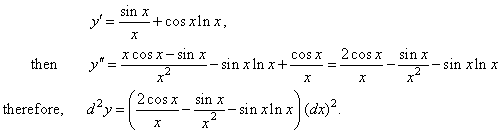 |
|
| |