|
|
Applications
of differentiation - the graph of a function and its derivative |
L'Hospital's
rule - limits of indeterminate forms |
|
Applications
of L'Hospital's
rule - evaluation of limits of indeterminate forms, examples |
|
|
|
|
|
|
| L'Hospital's
rule - limits of indeterminate forms |
| The
rule, based on the generalized mean value theorem, that enables the
evaluation of the limit of an indeterminate
quotient of functions as the quotient of limits of their derivatives is
called L'Hospital's rule. |
| a)
Indeterminate
forms |
 |
|
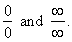| Let
f
and g
are differentiable functions near a
(except possibly at a)
and g'(x) is
not
0,
and if |
 |
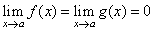| or |
 |
|
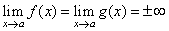| then |
 |
|
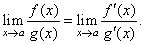| The
rule can also be applied in case when a
= oo. |
| If
the quotient of the derivatives repeats an indeterminate form
then we can proceed with the quotients of successive
derivatives, provided required conditions hold. |
| Another
indeterminate
forms |
| b)
Indeterminate form
0 · oo |
| Write
the product f (x)
· g
(x),
where |
 |
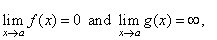as
a quotient |
|
 |
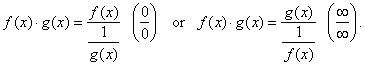| c)
Indeterminate form
oo
-
oo |
| Rewrite
given difference f (x)
-
g
(x)
into the product |
 |
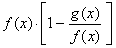and
first solve the indeterminate |
|
| form |
 |
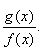If |
 |
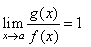then,
write the above product as |
|
 |
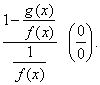| d)
Indeterminate (or indefinite) powers,
1oo,
00
and oo0
we solve taking the natural logarithm of the given expression
by writing |
| f (x)g
(x)
= y
or
ln
y
=
g
(x)
·
ln
f (x) |
| so
it then becomes an indeterminate product. |
| There
are cases where we should combine both L'Hospital's rule and elementary
methods to evaluate limits. |
|
|
Applications of L'Hospital's
rule - evaluation of limits of indeterminate forms, examples |
| Example:
Evaluate
the following limit |
 |
|
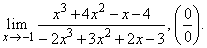| Solution:
|
 |
|
|
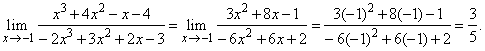| Example:
Evaluate
the following limit |
 |
|
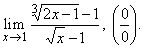| Solution:
|
 |
|
|
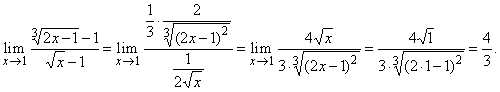| Example:
Evaluate
the following limit |
 |
|
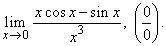| Solution:
|
 |
|
|
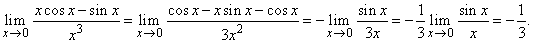| Example:
Evaluate
the following limit |
 |
|
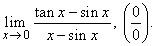| Solution:
|
 |
|
 |
|
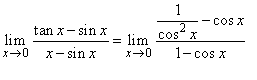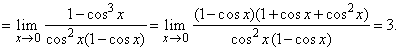| Example:
Evaluate
the following limit |
 |
|
|
|
|
|
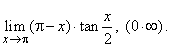| Example:
Evaluate
the following limit |
 |
|
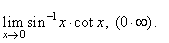| Solution:
|
 |
|
|
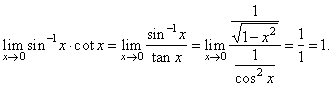| Example:
Evaluate
the following limit |
 |
|
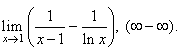| Solution:
|
 |
|
|
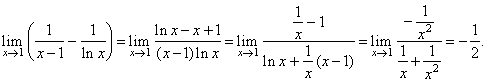| Example:
Evaluate
the following limit |
 |
|
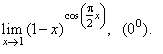| Solution:
|
 |
|
 |
| |
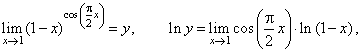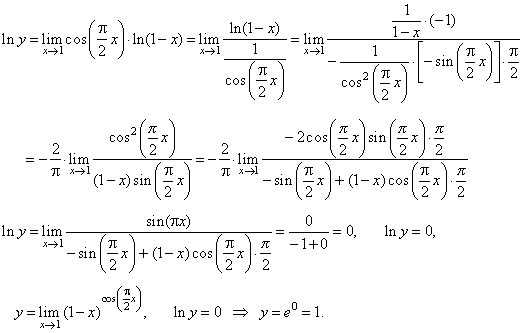| Example:
Evaluate
the following limit |
 |
|
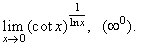| Solution:
|
 |
|
 |
|
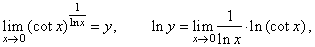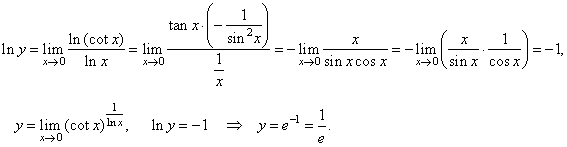| Example:
Evaluate
the following limit |
 |
|
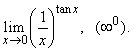| Solution:
|
 |
|
 |
|
|
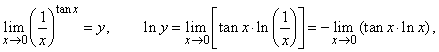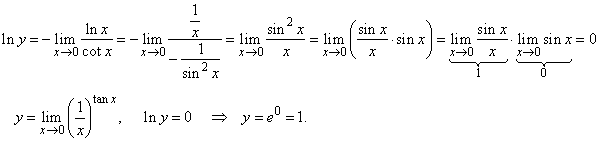