|
|
|
|
Applications of the derivative |
 Tangent,
normal, subtangent and subnormal
Tangent,
normal, subtangent and subnormal |
|
Property of the parabola |
|
Property
of power functions |
|
Property
of the exponential function |
|
|
|
|
|
|
| Tangent,
normal, subtangent and subnormal |
| A
segment of a tangent to a curve lying between the tangency point (the
point at which a tangent is drawn to a
curve) and the intercept of the tangent with the x-axis
is called the length of the tangent. |
| A
segment of the x-axis
lying between the x-coordinate
of the tangency point and the intercept of the tangent with
the axis is called the sub tangent. |
| Therefore,
the sub tangent is the projection of the segment of the tangent onto the x-axis. |
| A
segment of a line normal to a tangent lying between the tangency point
and the intercept of the normal with the x-axis
is called the length of the normal. |
| A
segment of the x-axis
lying between the x-coordinate
of the tangency point and the intercept of the normal with
the axis is called the subnormal. |
| Therefore,
the subnormal is the projection of the segment of the normal onto the x-axis. |
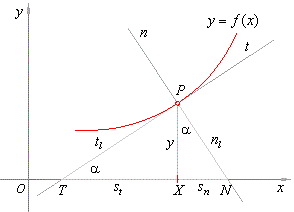
| In
the figure below denoted are, |
| the
length of the tangent tl
= PT,
the subtangent st
= TX, |
| the
length of the normal nl
= PN
and the subnormal sn
= NX. |
 |
| In
the right triangle PTX, |
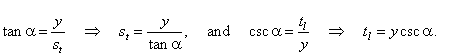 |
|
|
| In
the right triangle PNX, |
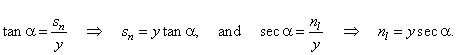 |
|
| Therefore,
the subtangent, |
and
the subnormal |
|
|
|
| The
length of the tangent, |
and
the
length of the normal |
|
|
|
|
| |
| At
every point of the parabola y2
= 2px the subnormal have the
same value p. |
| By
differentiating both sides of the equation of the parabola with
respect to x
we get |
| 2yy'
= 2p
or yy'
= p = sn. |
| We use this property to construct the normal and
the tangent at a point of the parabola. |
| Thus,
the normal line passes through the given point P(x,
y) of the
parabola
and the point x
+ p,
lying on the x-axis. |
| Further,
since |
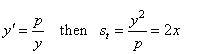 |
|
|
 |
|
| therefore,
the
vertex of the parabola y2
= 2p bisects the sub
tangent. |
|
| Property
of power functions |
| The
sub tangent of the power function y
= axn,
where n
is a positive integer, |
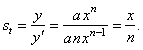 |
|
| Thus
for example, the tangent to the parabola y
= ax2
at P
(x,
y)
bisects the abscissa of P
that is,
st
= x/2,
as
shows the figure below. |
|
|
|
| Property
of the exponential function |
| The
sub tangent of the exponential function
y
= erx,
r
Î
R and r ¹
0, since |
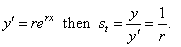 |
|
| Thus
for example, at every point of the exponential function
y
= ex the
sub tangent st
= 1,
as shows the figure
above. |